题目内容
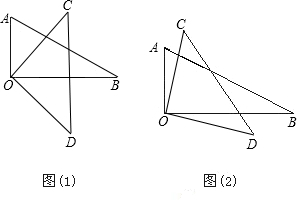 把一副三角板的直角顶点O重叠在一起.
把一副三角板的直角顶点O重叠在一起.(1)如图(1),当OB平分∠COD时,则∠AOD与∠BOC的和是多少度?
(2)如图(2),当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
(3)当∠BOC的余角的4倍等于∠AOD,则∠BOC多少度?
考点:余角和补角,角平分线的定义
专题:
分析:(1)根据角平分线的性质可得∠BOC=∠BOD=45°,根据角的和差可得∠AOC=90°-45°=45°,再根据角的和差可得∠AOD+∠BOC;
(2)根据角的和差关系可得∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=(∠AOC+∠BOC)+(∠BOD+∠BOC),依此即可求解;
(3)可得方程∠AOD+∠BOC=180°,∠AOD=180°-∠BOC,联立即可求解.
(2)根据角的和差关系可得∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=(∠AOC+∠BOC)+(∠BOD+∠BOC),依此即可求解;
(3)可得方程∠AOD+∠BOC=180°,∠AOD=180°-∠BOC,联立即可求解.
解答:解:(1)当OB平分∠COD时,有∠BOC=∠BOD=45°,
于是∠AOC=90°-45°=45°,
所以∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°;
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC,
所以∠AOD+∠BOC=90°+90°=180°.
(3)由上得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC,
180°-∠BOC=4(90°-∠BOC),
所以∠BOC=60°.
于是∠AOC=90°-45°=45°,
所以∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°;
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC,
所以∠AOD+∠BOC=90°+90°=180°.
(3)由上得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC,
180°-∠BOC=4(90°-∠BOC),
所以∠BOC=60°.
点评:考查了角平分线的定义,角度的计算.根据角平分线定义得出所求角与已知角的关系转化求解.注意一副三角板的直角顶点O重叠在一起时角的关系.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
下列计算正确的是( )
A、
| ||||||
B、3×
| ||||||
C、
| ||||||
D、
|
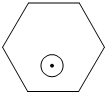 如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )| A、πr2 | ||||
B、
| ||||
C、2
| ||||
D、
|
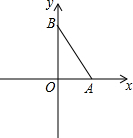 如图,点A、B分别在两条坐标轴上,且AB=2BO,在坐标轴上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )
如图,点A、B分别在两条坐标轴上,且AB=2BO,在坐标轴上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )| A、5个 | B、6个 | C、7个 | D、8个 |
 如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M.
如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M. 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H. 如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4
如图,等腰Rt△ABC中,∠ABC=90°,O是△ABC内一点,OA=6,OB=4