题目内容
4.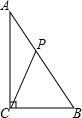 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )| A. | 5 | B. | 5或8 | C. | $\frac{5}{2}$ | D. | 4或$\frac{5}{2}$ |
分析 没有指明等腰三角形的底边,所以需要分类讨论:AP=AC,AP=PC,AC=PC.
解答  解:如图,∵在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,
解:如图,∵在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,
∴由勾股定理,得BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6cm.
①当AP=AC时,2t=8,则t=4;
②当AP=PC时,过点P作PD⊥AC于点D,则AD=CD,PD∥BC,
∴PD是△ABC的中位线,
∴点P是AB的中点,
∴2t=5,即t=$\frac{5}{2}$;
③若AC=PC=8cm时,与PC<AC矛盾,不和题意.
综上所述,t的值是4或$\frac{5}{2}$;
故选:D.
点评 本题考查了等腰三角形的判定,注意要分类讨论,还要注意PC的取值范围.

练习册系列答案
相关题目
14.不改变分式的值,下列各式中成立的是( )
| A. | $\frac{-a+5}{-a-5}=\frac{a+5}{a-5}$ | B. | $\frac{1}{-x+6}=\frac{-1}{x+6}$ | ||
| C. | $\frac{-x+y}{-x-y}=-\frac{x-y}{x+y}$ | D. | $\frac{-x}{y-3x}=\frac{x}{3x-y}$ |
19.下列三个结论中正确的是( )
| A. | 2<$\sqrt{6}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{6}$ | C. | $\root{3}{7}$<2$<\sqrt{6}$ | D. | $\root{3}{7}$<$\sqrt{6}$<2 |
16. 某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
(说明:40---55分为不合格,55---70分为合格,70---85分为良好,85---100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=18,b=0.5;c=3;d=0.05
(2)请根据频数分布表,画出相应的频数分布直方图.
 某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表| 成绩 | 划记 | 频数 | 百分比 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 | c | d | |
| 合计 |
(1)表中的a=18,b=0.5;c=3;d=0.05
(2)请根据频数分布表,画出相应的频数分布直方图.
13. 如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )| A. | 城 | B. | 市 | C. | 卫 | D. | 生 |
14. 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系后△ABC的顶点均在格点上.