题目内容
15.某农户经销一种农产品,已知该产品的进价为每千克20元,调查发现,该产品每天的销量y(千克)与售价x(元/千克)有如下关系:y=-2x+80,设该产品每天的销售利润为w元.(1)售价为多少时,每天的销售利润最大?最大利润是多少?
(2)物价部门规定该产品的售价不得高于28元/千克,该农户若每天获利150元,售价应定为多少?
分析 (1)利用每千克利润×销量=总利润,进而利用配方法求出二次函数最值;
(2)利用w=150,进而解方程得出答案.
解答 解:(1)由题意可得:
w=(x-20)(-2x+80)
=-2x2+120x-1600
=-2(x-30)2+200,
∵-2<0,
∴x=30时,w有最大值200,
答:售价为30元/千克时,每天的销售利润最大,最大利润是200元;
(2)当w=150时,可得-2(x-30)2+200=150,
解得:x1=25,x2=35,
∵35>28,
∴x2=35不合题意,应舍去,
答:该农户若要每天获利150元,售价应定为每千克25元.
点评 此题主要考查了二次函数的应用以及一元二次方程的解法,正确得出w与x之间的函数关系是解题关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
5.安岳县柠檬种植面积26万亩,柠檬产量12万吨,占全国80%以上,用科学记数法表示安岳县柠檬种植面积( )亩.
| A. | 2.6×103 | B. | 2.6×104 | C. | 2.6×105 | D. | 26×105 |
10.如图是一个数值运算程序,当输入值为-1时,则输出的数值为( )


| A. | 123 | B. | 121 | C. | 11 | D. | 3 |
4.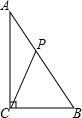 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
 如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )| A. | 5 | B. | 5或8 | C. | $\frac{5}{2}$ | D. | 4或$\frac{5}{2}$ |
5. 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | 20 | B. | $10\sqrt{2}$ | C. | 18 | D. | $20\sqrt{2}$ |