题目内容
已知△ABC三边长分别为6cm，8cm，10cm，则△ABC的内切圆的面积为 ．
考点：三角形的内切圆与内心,勾股定理的逆定理
专题：
分析：首先根据勾股定理求出直角三角形的斜边，再根据内切圆的半径等于两条直角边的和与斜边的差的一半进行计算，即可求得半径，然后利用圆的面积公式求解．
解答：解：∵直角三角形斜边为
=10（cm），
∴其内切圆的半径为：
=2，
则内切圆的面积是4πcm2．
故答案是：4πcm2．
| 62+82 |
∴其内切圆的半径为：
| 6+8-10 |
| 2 |
则内切圆的面积是4πcm2．
故答案是：4πcm2．
点评：此题主要考查了三角形内切圆半径求法，记住直角三角形的内切圆半径等于两直角边的和与斜边之差的一半这个结论是解题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
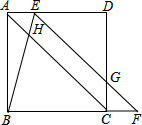如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连接EF与边CD相交于点G，连接BE与对角线AC相交于点H，AE=CF，BE=EG．
在三角形纸片ABC中，底角∠A=30°，将纸片的一角对折，使点A落在△ABC内，若∠2=20°，则∠1=若(a+
)2与|b+1|互为相反数，则的值为b-a=（ ）
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、1-
|