题目内容
在三角形纸片ABC中，底角∠A=30°，将纸片的一角对折，使点A落在△ABC内，若∠2=20°，则∠1=考点：三角形内角和定理,翻折变换（折叠问题）
专题：
分析：在△ADE中利用内角和定理，即可求得∠AED与∠ADE的和，又由四边形的内角和为360°，求得∠1的度数．
解答：解：如图，
∵在△ADE中，∠A+∠3+∠4=180°，
∴∠3+∠4=150°，
∵在四边形BCDE中，∠B+∠C+∠1+∠3+∠4+∠2=360°，
∴∠1+∠2=60°，
∵∠2=20°，
∴∠1=40°．
故答案为：40°．
∵在△ADE中，∠A+∠3+∠4=180°，
∴∠3+∠4=150°，
∵在四边形BCDE中，∠B+∠C+∠1+∠3+∠4+∠2=360°，
∴∠1+∠2=60°，
∵∠2=20°，
∴∠1=40°．
故答案为：40°．
点评：此题考查三角形的内角和定理：三角形的内角和是180°，以及四边形的内角和是360°．
练习册系列答案
相关题目
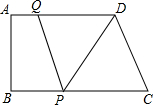如图所示，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=6，BC=24，AD=16．动点P从点C出发，沿射线CB的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
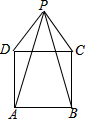如图，P为正方形ABCD外一点，且∠PAD=∠PBC=15°，求证：△PDC为等边三角形．