题目内容
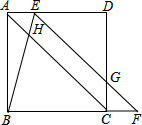 如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;
(2)求∠BEF大小;
(3)若EB=4,则△BAE的面积为
考点:正方形的性质
专题:
分析:(1)利用平行四边形的判定及其性质定理即可解决问题;
(2)作辅助线构造出一对全等三角形,利用等边三角形的判定及其性质即可解决问题;
(3)借助旋转变换将△BCG与△BAE拼接到一起,通过作辅助线求出△BHE的高,问题即可解决.
(2)作辅助线构造出一对全等三角形,利用等边三角形的判定及其性质即可解决问题;
(3)借助旋转变换将△BCG与△BAE拼接到一起,通过作辅助线求出△BHE的高,问题即可解决.
解答:解:(1)∵四边形ABCD是正方形,
∴AE∥CF,
又∵AE=CF,
∴四边形AEFC是平行四边形,
故EF∥AC.
(2)连接BG
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
,
∴△ABE≌CBG(SAS),
∴BE=BG;
又∵BE=EG,
∴BE=BG=EG,△BEG是等边三角形,
故∠BEF=60°.
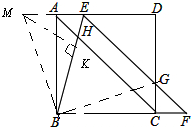 (3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;
(3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;
∵△BEG是等边三角形,
∴∠EBG=60°,
∴∠ABE+∠CBG=90°-60°=30°;
在△ABM与△BCG中,
,
∴△ABM≌△BCG(SAS),
∴BM=BC=4,∠ABM=∠CBG;
故∠ABM+∠ABE=∠ABE+∠CBG=30°,
∴MK=
BH=2,
∴△BME的面积=
×4×2=4,△BAE的面积═
×4=2.
∴AE∥CF,
又∵AE=CF,
∴四边形AEFC是平行四边形,
故EF∥AC.
(2)连接BG
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
|
∴△ABE≌CBG(SAS),
∴BE=BG;
又∵BE=EG,
∴BE=BG=EG,△BEG是等边三角形,
故∠BEF=60°.
 (3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;
(3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;∵△BEG是等边三角形,
∴∠EBG=60°,
∴∠ABE+∠CBG=90°-60°=30°;
在△ABM与△BCG中,
|
∴△ABM≌△BCG(SAS),
∴BM=BC=4,∠ABM=∠CBG;
故∠ABM+∠ABE=∠ABE+∠CBG=30°,
∴MK=
| 1 |
| 2 |
∴△BME的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查了正方形的性质、全等三角形的判定及其应用问题;解题的关键是通过作辅助线构造出全等三角形,结合等边三角形的判定及其性质来解决问题;对综合运用能力及探究思维能力提出了较高的要求.

练习册系列答案
相关题目