题目内容
8. 如图,若△ABC≌△ADE,且∠B=60°,∠C=20°则∠DAE=100°.
如图,若△ABC≌△ADE,且∠B=60°,∠C=20°则∠DAE=100°.
分析 根据全等三角形的性质求出∠ADE=∠B=60°,∠E=∠C=20°,根据三角形内角和定理求出即可.
解答 解:∵△ABC≌△ADE,∠B=60°,∠C=20°,
∴∠ADE=∠B=60°,∠E=∠C=20°,
∴∠DAE=180°-∠ADE-∠E=180°-60°-20°=100°,
故答案为:100°.
点评 本题考查了全等三角形的性质和三角形内角和定理的应用,能根据全等三角形的性质求出∠ADE=∠B,∠E=∠C是解此题的关键,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
20.已知△ABC≌△DEF,那么EF的对应边是( )
| A. | AB | B. | BC | C. | CA | D. | DE |
17.已知,⊙O的半径为5cm,点P到圆心O的距离为4cm,则点P在⊙O的( )
| A. | 外部 | B. | 内部 | C. | 圆上 | D. | 不能确定 |
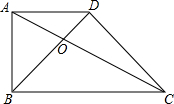 如图,已知梯形ABCD,AD∥BC,对角线AC与BD相交于点O,S△AOD=9,S△BOC=16,求S梯形ABCD.
如图,已知梯形ABCD,AD∥BC,对角线AC与BD相交于点O,S△AOD=9,S△BOC=16,求S梯形ABCD.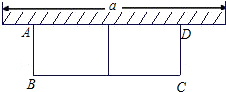 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2). 如图,若数轴上A、B两点所对应的有理数分别为a、b,则|b|-|a|=<0.
如图,若数轴上A、B两点所对应的有理数分别为a、b,则|b|-|a|=<0.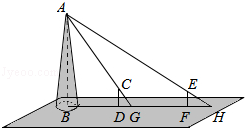 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.