题目内容
3.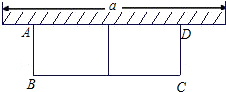 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).(1)求S与x之间的函数关系式;
(2)如果要围成面积为45m2的花园,AB的长是多少米?
(3)能围成面积比45m2更大的花园吗?如果能,请求出最大面积.并说明围法;如果不能,请说明理由.
分析 (1)根据AB为xm,BC就为(24-3xm),利用长方体的面积公式,可求出关系式.
(2)将s=45m代入(1)中关系式,可求出x即AB的长.
(3)利用配方法求得最大面积即可.
解答 解:(1)根据题意,得S=x(24-3x),
即所求的函数解析式为:S=-3x2+24x,
(2)根据题意,设AB长为x,则BC长为24-3x,
则-3x2+24x=45.
整理,得x2-8x+15=0,
解得x=3或5,
当x=3时,BC=24-9=15>13不成立,
当x=5时,BC=24-15=9<13成立,
∴AB长为5m;
(3)S=24x-3x2=-3(x-4)2+48
∵墙的最大可用长度为13m,
∴当x=4,有最大面积为48m2.此时24-3x=12<13
∴能围成最大面积为48m2的正方形花园,其长和宽分别为12m、4m.
点评 此题考查了二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题的关键是垂直于墙的有三道篱笆.

练习册系列答案
相关题目
15. 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
 数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )
数a、b在数轴上的位置如图所示,化简a-|b-a|的结果为( )| A. | 2a-b | B. | b-2a | C. | -b | D. | b |
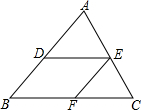 如图,DE∥BC,EF∥AB,则:
如图,DE∥BC,EF∥AB,则: 如图,若△ABC≌△ADE,且∠B=60°,∠C=20°则∠DAE=100°.
如图,若△ABC≌△ADE,且∠B=60°,∠C=20°则∠DAE=100°.