题目内容
如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，（1）求∠ABD的度数；
（2）若菱形的边长为2，求菱形的面积．
考点：菱形的性质
专题：
分析：（1）根据菱形的性质可得到AD=BD，AD=AB，从而可推出△ABD是等边三角形，从而不难求得∠ABD的度数．
（2）根据勾股定理可求得DE的长，再根据菱形的面积公式即可求得菱形的面积．
（2）根据勾股定理可求得DE的长，再根据菱形的面积公式即可求得菱形的面积．
解答：
解：（1）∵DE⊥AB，AE=BE
∴△ABD是等腰三角形，
∴AD=BD
∵四边形ABCD是菱形
∴AD=AB
∴AD=AB=BD，
∴△ABD是等边三角形
∴∠ABD=60°；
（2）∵AD=AB=2，
∴AE=1，
在Rt△AED中，DE=
=
，
∴S菱形ABCD=AB•DE=2
．
解：（1）∵DE⊥AB，AE=BE∴△ABD是等腰三角形，
∴AD=BD
∵四边形ABCD是菱形
∴AD=AB
∴AD=AB=BD，
∴△ABD是等边三角形
∴∠ABD=60°；
（2）∵AD=AB=2，
∴AE=1，
在Rt△AED中，DE=
| 22-12 |
| 3 |
∴S菱形ABCD=AB•DE=2
| 3 |
点评：本题考查的是菱形的性质，熟知菱形的四条边相等是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，∠1=∠ACB，∠2=∠3，FH⊥AB于H．问CD与AB有什么关系？并说明理由．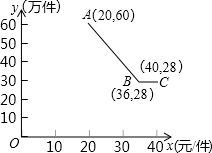
淮安华宇公司获得授权生产某种奥运纪念品，经市场调查分析，该纪念品的销售量y1（万件）与纪念品的价格x（元/件）之间的函数图象如图，该公司纪念品的生产数量y2（万件）与纪念品的价格x（元/件）近似满足函数关系式y2=-