题目内容
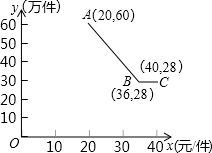 淮安华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量y1(万件)与纪念品的价格x(元/件)之间的函数图象如图,该公司纪念品的生产数量y2(万件)与纪念品的价格x(元/件)近似满足函数关系式y2=-
淮安华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量y1(万件)与纪念品的价格x(元/件)之间的函数图象如图,该公司纪念品的生产数量y2(万件)与纪念品的价格x(元/件)近似满足函数关系式y2=-| 3 |
| 2 |
请解答下列问题:
(1)求y1与x的函数关系式,并写出x的取值范围;
(2)若每件纪念品的成本为15元,则价格应定为多少元时,能获得最大利润?并求出此时的最大利润.
考点:二次函数的应用
专题:
分析:(1)此函数为分段函数,所以要按照自变量的取值范围来不同对待,可根据图中的信息运用待定系数法求出函数的关系式;
(2)根据(1)中的函数关系式以及自变量的取值范围的不同分别根据利润=每一件的销售利润×销售件数列出函数解析式,利用性质探讨答案即可.
(2)根据(1)中的函数关系式以及自变量的取值范围的不同分别根据利润=每一件的销售利润×销售件数列出函数解析式,利用性质探讨答案即可.
解答:解:(1)当20≤x≤36时,
设y1与x的函数解析式为:y=kx+b,将点A(20,60)、B(36,28)代入y=kx+b得:
.
解得:
,
∴y1与x的函数关系式为:y1=-2x+100;
当36≤x≤40时,
y1=28.
(2)设销售总利润为W,
当20≤x≤36时,
W=(-2x+100)(x-15)=-2x2+130x-1500=-2(x-
)2+612.5;
当x=32.5时,y最大值为612.5;
当36≤x≤40时,
W=(-
x+85)(x-15)=-
x2+
x-1245,
a<0,
当36≤x≤40,y随着x的增大而减小,所以当x=36时,y最大为651.
因此价格应定为36元时,能获得最大利润,此时的最大利润是651万元.
设y1与x的函数解析式为:y=kx+b,将点A(20,60)、B(36,28)代入y=kx+b得:
|
解得:
|
∴y1与x的函数关系式为:y1=-2x+100;
当36≤x≤40时,
y1=28.
(2)设销售总利润为W,
当20≤x≤36时,
W=(-2x+100)(x-15)=-2x2+130x-1500=-2(x-
| 65 |
| 2 |
当x=32.5时,y最大值为612.5;
当36≤x≤40时,
W=(-
| 3 |
| 2 |
| 3 |
| 2 |
| 215 |
| 2 |
a<0,
当36≤x≤40,y随着x的增大而减小,所以当x=36时,y最大为651.
因此价格应定为36元时,能获得最大利润,此时的最大利润是651万元.
点评:此题考查二次函数的实际运用,借助函数图象表达题目中的信息,读懂图象是关键.本题要注意分段函数的性质和应用.

练习册系列答案
相关题目
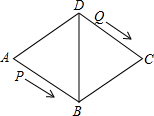 如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
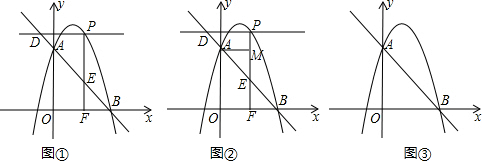
 如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,