题目内容
20.对某羽毛球的质量进行随机抽查,结果如下表所示:| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
(2)根据上表,从这批羽毛球中任取一个,为优等品的概率约为0.9;
(3)小明认为,从这批羽毛球中抽取10个,优等品的数量至少为8个,他的说法正确吗?为什么?
分析 (1)根据表格中的数据可以求得a的值;
(2)根据表格中的数据可以得到优等品的概率;
(3)首先,根据概率的知识可以判断小明的说法是否正确,然后说明理由即可.
解答 解:(1)由题意可得,
a=450÷500=0.9,
故答案为:0.9;
(2)根据表格中的数据,可知从这批羽毛球中任取一个,为优等品的概率约为0.9,
故答案为:0.9;
(3)小明的说法不正确,
因为题目中表格的数据反映的是优等品出现的概率,也就是可能性大小,从这批羽毛球中抽取10个,可能都是优等品,也可能都不是优等品,故小明的说法错误.
点评 本题考查利用频率估计概率,解答本题的关键是明确概率的定义,利用概率的知识解答.

练习册系列答案
相关题目
15.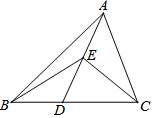 如图,已知△ABC中,D是BC上一点,E是AD的中点,若△BEC的面积为15,则△ABC的面积为( )
如图,已知△ABC中,D是BC上一点,E是AD的中点,若△BEC的面积为15,则△ABC的面积为( )
 如图,已知△ABC中,D是BC上一点,E是AD的中点,若△BEC的面积为15,则△ABC的面积为( )
如图,已知△ABC中,D是BC上一点,E是AD的中点,若△BEC的面积为15,则△ABC的面积为( )| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
5.如图,是用棋子摆成的图案,摆第①个图案需要7枚棋子,摆第②个图案需要12枚棋子,摆第③个图案需要19枚棋子,摆第④个图案需要28枚棋子,…,按照这样的规律,则摆第n个图案需要n2+2n+4枚棋子.

9.下列方程中,一定是一元二次方程的是( )
| A. | 2x2-7=3y+1 | B. | 5x2-$\frac{1}{x}$-2=0 | C. | $\frac{1}{3}$x-5=$\frac{{x}^{2}}{2}$ | D. | ax2+bx+c=0 |
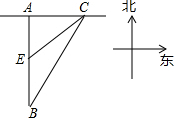 阅读材料,回答问题
阅读材料,回答问题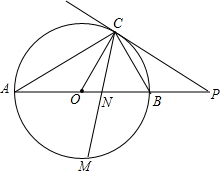 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.