题目内容
12.计算(1)8+(-$\frac{1}{4}$)-5-(-0.25)
(2)-10+8÷(-2)-4×(-5)
(3)($\frac{1}{3}$+$\frac{1}{9}$-$\frac{5}{12}$)×(-36)
(4)(-1)2×2+(-2)3÷4
(5)8a+2b+(5a-b)
(6)(2x2-xy+7)-(-4x2+2xy+7)
分析 (1)先写成省略括号的形式,再计算即可;
(2)先算乘除,后算加减即可;
(3)利用乘法分配律先算乘法,然后计算加减即可;
(4)先算乘法、后算乘除,最后计算加减即可;
(5)首先去括号,再合并同类项即可;
(6)首先去括号,再合并同类项即可.
解答 解:(1)原式=8-$\frac{1}{4}$-5+$\frac{1}{4}$=8-5=3;
(2)原式=-10-4+20=6;
(3)原式=-12-4+15=-16+15=-1;
(4)原式=1×2-8÷4=2-2=0;
(5)原式=8a+2b+5a-b=13a+b;
(6)原式=2x2-xy+7+4x2-2xy-7=6x2-3xy.
点评 此题主要考查了有理数的混合运算和整式的加减,关键是掌握有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.

练习册系列答案
相关题目
20.对某羽毛球的质量进行随机抽查,结果如下表所示:
(1)表中a的值为0.9;
(2)根据上表,从这批羽毛球中任取一个,为优等品的概率约为0.9;
(3)小明认为,从这批羽毛球中抽取10个,优等品的数量至少为8个,他的说法正确吗?为什么?
| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
(2)根据上表,从这批羽毛球中任取一个,为优等品的概率约为0.9;
(3)小明认为,从这批羽毛球中抽取10个,优等品的数量至少为8个,他的说法正确吗?为什么?
17.正方形具有而矩形不具有的性质是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相垂直 |
 如图,在△ABC中,∠B=25°,∠C=30°.
如图,在△ABC中,∠B=25°,∠C=30°.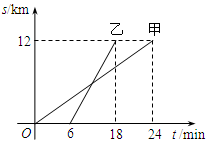 甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米.
甲、乙两人以相同路线前往离学校12km的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,求每分钟乙比甲多行驶多少千米.