题目内容
10．关于x的一元二次方程（x-3）（x-2）-m2=0，求证：无论m取何值，方程总有两个不相等的实数根．（提示：先化为一般形式，c=6-m2）分析 将原方程变形为一般式，由根的判别式可得出△=4m2+1＞0，由此即可证出无论m取何值，方程总有两个不相等的实数根．
解答 证明：原方程可变形为x2-5x+6-m2=0．
△=（-5）2-4×（6-m2）=4m2+1，
∵m2≥0，
∴4m2+1＞0，即△＞0，
∴无论m取何值，方程总有两个不相等的实数根．
点评 本题考查了根的判别式，牢记“当△＞0时，方程有两个不相等的实数根”是解题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
20．对某羽毛球的质量进行随机抽查，结果如下表所示：
（1）表中a的值为0.9；
（2）根据上表，从这批羽毛球中任取一个，为优等品的概率约为0.9；
（3）小明认为，从这批羽毛球中抽取10个，优等品的数量至少为8个，他的说法正确吗？为什么？
| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
（2）根据上表，从这批羽毛球中任取一个，为优等品的概率约为0.9；
（3）小明认为，从这批羽毛球中抽取10个，优等品的数量至少为8个，他的说法正确吗？为什么？
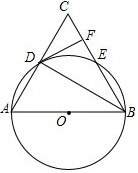如图，在△ABC中，以点AB为直径的⊙O分别与AC、BC相交于D、E两点，且AD=CD，过点D作⊙O的切线交BC于点F．
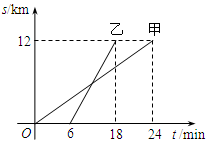甲、乙两人以相同路线前往离学校12km的地方参加植树活动．图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s（km）随时间t（min）变化的函数图象，求每分钟乙比甲多行驶多少千米．
如图，正方形ABCD的边长为6$\sqrt{2}$，点E是边CD的中点，点F在边BC上，AE、AF分别与对角线BD交于点G、H，点M、N分别是线段GH、EF的中点，若∠EAF=45°，则线段MN的长为$\frac{5}{2}$．