题目内容
17.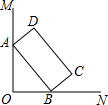 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.
分析 取AB的中点E,连接OE、DE、OD,根据三角形的任意两边之和大于第三边可知当O、D、E三点共线时,点D到点O的距离最大,再根据勾股定理求出DE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.
解答 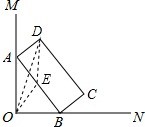 解:如图,取AB的中点E,连接OE、DE、OD,
解:如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=8,BC=3,
∴OE=AE=$\frac{1}{2}$AB=4,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴OD的最大值为:5+4=9;
故答案为:9.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O、E、D三点共线时,点D到点O的距离最大是解题的关键.

练习册系列答案
相关题目
12.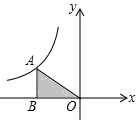 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )
 如图所示,S△ABO=2,则反比例函数的解析式是( )
如图所示,S△ABO=2,则反比例函数的解析式是( )| A. | $y=-\frac{2}{x}$ | B. | $y=\frac{2}{x}$ | C. | $y=-\frac{4}{x}$ | D. | $y=\frac{4}{x}$ |
9.下列每组数据中的三个数值分别为三角形的三边长,不能构成直角三角形是( )
| A. | 4,6,8 | B. | 9,40,41 | C. | 5,12,13 | D. | 7,24,25 |
 △ABC中,∠A=40°,∠B:∠C=1:6,求∠B的度数.
△ABC中,∠A=40°,∠B:∠C=1:6,求∠B的度数. 如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.
如图,△ABC中,AC=BC,AC⊥BC,E为△ABC外一点,且∠CEA=45°,求证:AE⊥BE.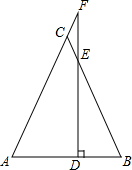 如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.
如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.