题目内容
2.菱形具有而矩形不具有的性质是( )| A. | 两组对边分别平行 | B. | 对角线互相垂直 | ||
| C. | 两组对角分别相等 | D. | 对角线互相平分 |
分析 由矩形和菱形的性质容易得出结论.
解答 解:A、两组对边分别平行是平行四边形的基本性质,两者都具有,故A不符合题意;
B、菱形的对角线互相垂直,而矩形的对角线不一定互相垂直;故B符合题意;
C、两组对边分别平行是平行四边形的基本性质,两者都具有,故C不符合题意;
D、对角线互相平分是平行四边形的基本性质,两者都具有,故D不符合题意;
故选:B.
点评 此题主要考查了菱形的性质以及平行四边形和矩形的性质,正确区分它们的性质是解题关键.

练习册系列答案
相关题目
4.下列各数中,-3的倒数是( )
| A. | 3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -3 |
10.若二次函数y=-x2-3x+2的自变量x分别取x1、x2、x3,且x1、x2、x3,且0<x1<x2<x3,则对应的函数值y1、y2、y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y1<y3<y2 | D. | y2<y3<y1 |
7.如图,若AB∥CD,则α、β,γ之间的关系为( )


| A. | α+β+γ=360° | B. | α+β-γ=180° | C. | α+β+γ=180° | D. | α-β+γ=180° |
14.若直线y=kx+b平行于直线y=3x-4,且过点(1,-2),则该直线的解析式是( )
| A. | y=3x-2 | B. | y=-3x-6 | C. | y=3x-5 | D. | y=3x+5 |
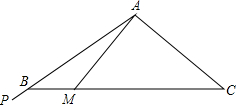 在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.
在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm. 如图,在△ABC中,∠ACB=90°,将△ABC绕点C,按顺时针方向旋转得△A1B1C,且A1B1∥BC,∠ABB1=30°,求旋转角∠BCB1的大小.
如图,在△ABC中,∠ACB=90°,将△ABC绕点C,按顺时针方向旋转得△A1B1C,且A1B1∥BC,∠ABB1=30°,求旋转角∠BCB1的大小.