题目内容
设a、b、c为整数，且|a-b|+|c-b|=1，求|c-a|+|a-b|+|b-c|的值．
考点：绝对值
专题：
分析：由a、b、c为整数，且|a-b|+|c-b|=1，分两种情况①|a-b|=0，|c-b|=1，②|a-b|=1，|c-b|=0求解．
解答：解：∵a、b、c为整数，且|a-b|+|c-b|=1，
∴①|a-b|=0，|c-b|=1，即a=b，|c-b|=|c-a|=1，得出|c-a|+|a-b|+|b-c|=1+1=2，
②|a-b|=1，|c-b|=0，即c=b，|a-b|=|a-c|=|c-a|=1，得出|c-a|+|a-b|+|b-c|=1+1=2，
综上所述|c-a|+|a-b|+|b-c|=2．
∴①|a-b|=0，|c-b|=1，即a=b，|c-b|=|c-a|=1，得出|c-a|+|a-b|+|b-c|=1+1=2，
②|a-b|=1，|c-b|=0，即c=b，|a-b|=|a-c|=|c-a|=1，得出|c-a|+|a-b|+|b-c|=1+1=2，
综上所述|c-a|+|a-b|+|b-c|=2．
点评：本题主要考查了绝对值，解题的关键是分两种情况讨论求解．
练习册系列答案
阅读快车系列答案
相关题目
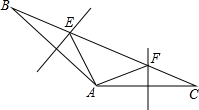如图，在△ABC中，边AB、AC的垂直平分线分别交BC于E、F．