题目内容
△ABC是⊙O的内接正三角形,P是
上一点.探索PA与PB+PC之间的数量关系,并说明理由.
 |
| BC |
考点:全等三角形的判定与性质,等边三角形的性质,圆周角定理
专题:
分析:作出图形,根据同弧所对的圆周角相等可得∠BAE=∠BCP,∠APB=∠ACB=60°,在PA上截取PE=BP,判断出△PBE是等边三角形,根据等边三角形的性质可得BE=PE=PB,再求出∠AEB=∠CPB=120°,根据等边三角形的三条边都相等可得AB=BC,然后利用“角角边”证明△ABE和△CBP全等,根据全等三角形对应边相等可得AE=PC,再根据PA=AE+PE等量代换即可得证.
解答: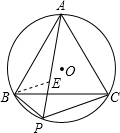 解:PA=PB+PC.
解:PA=PB+PC.
理由如下:如图,由圆周角定理得,∠BAE=∠BCP,∠APB=∠ACB=60°,
在PA上截取PE=BP,则△PBE是等边三角形,
所以BE=PE=PB,
∵∠AEB=180°-60°=120°,
∠CPB=120°,
∴∠AEB=∠CPB=120°,
∵△ABC是正三角形,
∴AB=BC,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(AAS),
∴AE=PC,
∵PA=AE+PE,
∴PA=PB+PC.
 解:PA=PB+PC.
解:PA=PB+PC.理由如下:如图,由圆周角定理得,∠BAE=∠BCP,∠APB=∠ACB=60°,
在PA上截取PE=BP,则△PBE是等边三角形,
所以BE=PE=PB,
∵∠AEB=180°-60°=120°,
∠CPB=120°,
∴∠AEB=∠CPB=120°,
∵△ABC是正三角形,
∴AB=BC,
在△ABE和△CBP中,
|
∴△ABE≌△CBP(AAS),
∴AE=PC,
∵PA=AE+PE,
∴PA=PB+PC.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,圆周角定理,作辅助线构造出等边三角形和全等三角形是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 如图,在等边△ABC中,将△BMN沿MN翻折,点B恰好落在AC边上的点E处,且AE:CE=1:3,则BM:BN=
如图,在等边△ABC中,将△BMN沿MN翻折,点B恰好落在AC边上的点E处,且AE:CE=1:3,则BM:BN= 如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=
如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,反比例函数y=