题目内容
在△ABC中,
(1)已知∠A=2∠C,∠B-∠C=60°,求∠B和∠C的大小;
(2)已知∠A=
∠B=
∠C,求△ABC各个内角的大小.
(1)已知∠A=2∠C,∠B-∠C=60°,求∠B和∠C的大小;
(2)已知∠A=
| 1 |
| 3 |
| 1 |
| 5 |
考点:三角形内角和定理
专题:
分析:(1)把∠A,∠B都用∠C表示,进一步利用三角形的内角和求得答案即可;
(2)把∠C,∠B都用∠A表示,进一步利用三角形的内角和求得答案即可.
(2)把∠C,∠B都用∠A表示,进一步利用三角形的内角和求得答案即可.
解答:解:(1)∵∠B-∠C=60°,
∴∠B=∠C+60°,
∵∠A+∠B+∠C=180°,
∴2∠C+∠C+60°+∠C=180°
∴∠C=30°,
∴∠B=∠C+60°=90°.
(2)∵∠A=
∠B=
∠C,
∴∠B=3∠A,∠C=5∠A,
∵∠A+∠B+∠C=180°,
∴∠A+3∠A+5∠A=180°
∴∠A=20°,
∴∠B=3∠A=60°,∠C=5∠A=100°.
∴∠B=∠C+60°,
∵∠A+∠B+∠C=180°,
∴2∠C+∠C+60°+∠C=180°
∴∠C=30°,
∴∠B=∠C+60°=90°.
(2)∵∠A=
| 1 |
| 3 |
| 1 |
| 5 |
∴∠B=3∠A,∠C=5∠A,
∵∠A+∠B+∠C=180°,
∴∠A+3∠A+5∠A=180°
∴∠A=20°,
∴∠B=3∠A=60°,∠C=5∠A=100°.
点评:此题考查三角形的内角和,解决问题的关键,是用一个角来表示其他角,进一步列方程解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
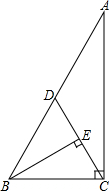 已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.
已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.