题目内容
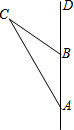 如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问:
如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问:(1)12:00时这艘船距离礁石多远?
(2)这艘船在什么时刻距离礁石最近?
考点:勾股定理的应用,方向角,等腰三角形的判定与性质
专题:
分析:(1)根据题意得出∠CAB=30°,∠CBF=60°,进而得出△CBE是等边三角形,求出EC的长即可;
(2)利用锐角三角函数关系得出BF的长,进而得出答案.
(2)利用锐角三角函数关系得出BF的长,进而得出答案.
解答: 解:(1)过点C作CF⊥AB于点F,使AB=BE,连接CE,
解:(1)过点C作CF⊥AB于点F,使AB=BE,连接CE,
由题意可得:AB=20海里,∠CAB=30°,∠CBF=60°,
故∠ACB=30°,即∠CAB=∠ACB,则BC=AB=20海里,
∵12:00时,船距离A点40海里,
∴BE=20海里,
∴BC=BE=20海里,又∠CBE=60°,
∴△CBE是等边三角形,
∴EC=20海里,
∴12:00时这艘船距离礁石20海里;
(2)由(1)得,∵CF⊥BE,∠CBF=60°,
∴FB=BCcos60°=20×
=10(海里),
即AF=30海里,
故这艘船上午8:00从A处出发,11时到达F点.
答:这艘船在11时距离礁石最近.
 解:(1)过点C作CF⊥AB于点F,使AB=BE,连接CE,
解:(1)过点C作CF⊥AB于点F,使AB=BE,连接CE,由题意可得:AB=20海里,∠CAB=30°,∠CBF=60°,
故∠ACB=30°,即∠CAB=∠ACB,则BC=AB=20海里,
∵12:00时,船距离A点40海里,
∴BE=20海里,
∴BC=BE=20海里,又∠CBE=60°,
∴△CBE是等边三角形,
∴EC=20海里,
∴12:00时这艘船距离礁石20海里;
(2)由(1)得,∵CF⊥BE,∠CBF=60°,
∴FB=BCcos60°=20×
| 1 |
| 2 |
即AF=30海里,
故这艘船上午8:00从A处出发,11时到达F点.
答:这艘船在11时距离礁石最近.
点评:此题主要考查了解直角三角形的应用,根据题意得出△CBE是等边三角形是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
以直角三角形的三边为边长分别向外作正方形,已知其中两个正方形的面积分别为20和16,则第三个正方形的边长为( )
A、2
| ||
| B、4或6 | ||
C、2
| ||
| D、2或6 |
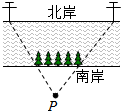 如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为
如图,一条河的两岸有一段平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆,小丽站在离南岸边15米的点P处看北岸,发现北岸相邻的两根电线恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为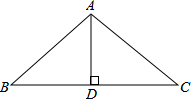 如图,在△ABC中,∠BAC=108°,AB=AC,AD⊥BC,垂足为D,求∠BAD的度数.
如图,在△ABC中,∠BAC=108°,AB=AC,AD⊥BC,垂足为D,求∠BAD的度数. 如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB为
如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB为 已知?AOBC在平面直角坐标系中的位置如图所示,点A,B的坐标分别为(3,4)(7,0),求点C的坐标.
已知?AOBC在平面直角坐标系中的位置如图所示,点A,B的坐标分别为(3,4)(7,0),求点C的坐标.