题目内容
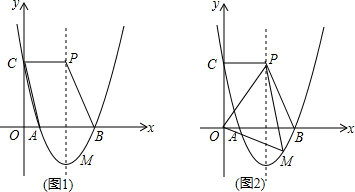
如图1,已知二次函数y=ax2-8ax+12(a>0)的图象与x轴分别交于A、B两点,与y轴交于点C,点P在抛物线的对称轴上,且四边形ABPC为平行四边形.
(1)求此抛物线的对称轴,并确定此二次函数的解析式;
(2)点M为x轴下方抛物线上一点,若△OMP的面积为36,求点M的坐标.
(1)求此抛物线的对称轴,并确定此二次函数的解析式;
(2)点M为x轴下方抛物线上一点,若△OMP的面积为36,求点M的坐标.

考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征,平行四边形的性质
专题:计算题
分析:(1)利用二次函数的性质可得对称轴为直线x=4,则PC=4,再根据平行四边形的性质得PC=AB=4,然后利用抛物线的对称性可得A(2,0),B(6,0),然后把把点 A(2,0)代入得y=ax2-8ax+12求出a=1,所以二次函数解析式为y=x2-8x+12;
(2)根据二次函数图象上点的坐标特征,设M(m,x2-8x+12),其中2<m<6,作MN⊥y轴于N,如图2,利用S梯形CPMN-S△OCP-S△OMN=S△OPM得到
(4+m)(12-m2+8m-12)-
×4×12-
m(-m2+8m-12)=36,化简得:m2-11m+30=0,然后解方程求出m即可得到点M的坐标.
(2)根据二次函数图象上点的坐标特征,设M(m,x2-8x+12),其中2<m<6,作MN⊥y轴于N,如图2,利用S梯形CPMN-S△OCP-S△OMN=S△OPM得到
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)对称轴为直线x=-
解:(1)对称轴为直线x=-
=4,则PC=4,
∵四边形ABPC为平行四边形,
∴PC∥AB,PC=AB,
∴PC=AB=4,
∴A(2,0),B(6,0),
把点 A(2,0)代入得y=ax2-8ax+12得4a-16a+12=0,解得a=1,
∴二次函数解析式为y=x2-8x+12;
(2)设M(m,x2-8x+12),其中2<m<6,
作MN⊥y轴于N,如图2,
∵S梯形CPMN-S△OCP-S△OMN=S△OPM,
∴
(4+m)(12-m2+8m-12)-
×4×12-
m(-m2+8m-12)=36,
化简得:m2-11m+30=0,解得m1=5,m2=6,
∴点M的坐标为(5,-3).
 解:(1)对称轴为直线x=-
解:(1)对称轴为直线x=-| -8a |
| 2a |
∵四边形ABPC为平行四边形,
∴PC∥AB,PC=AB,
∴PC=AB=4,
∴A(2,0),B(6,0),
把点 A(2,0)代入得y=ax2-8ax+12得4a-16a+12=0,解得a=1,
∴二次函数解析式为y=x2-8x+12;
(2)设M(m,x2-8x+12),其中2<m<6,
作MN⊥y轴于N,如图2,
∵S梯形CPMN-S△OCP-S△OMN=S△OPM,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简得:m2-11m+30=0,解得m1=5,m2=6,
∴点M的坐标为(5,-3).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了二次函数的性质.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
若(-x)2=(-5)2,则x的值为( )
| A、±5 | B、5 | C、-5 | D、25 |
 如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长.
如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长.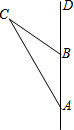 如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问:
如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问: