题目内容
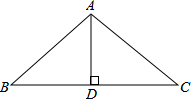如图，在△ABC中，∠BAC=108°，AB=AC，AD⊥BC，垂足为D，求∠BAD的度数．考点：等腰三角形的性质
专题：
分析：由等腰三角形的“三线合一”的性质可知AD平分∠BAC，可求得∠BAD．
解答：解：
∵AB=AC，AD⊥BC，
∴AD平分∠BAC，
∴∠BAD=
∠BAC=54°．
∵AB=AC，AD⊥BC，
∴AD平分∠BAC，
∴∠BAD=
| 1 |
| 2 |
点评：本题主要考查等腰三角形的性质，掌握等腰三角形底边上的中线、高和顶角的角平分线相互重合是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
若最简二次根式
与
是同类二次根式，则a、b的值为（ ）
| 3a-1 | 2a+5b |
| a-2b+8 |
| A、a=1，b=1 |
| B、a=2，b=-1 |
| C、a=-2，b=1 |
| D、a=-1，b=1 |
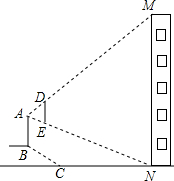如图，小明家居住的家属楼前20米处有一土丘，经测量斜坡长为8米，坡角恰好为30°．一天小明站在斜坡顶端B处，手持1米的木棒ED（手臂长为0.6米，手臂与身子垂直，木棒与身子平行），发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上；眼睛A、木棒的底端E、楼房的底部N三点共线，请你计算小明家居住的这栋楼的高度．（结果精确到1米，
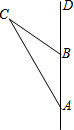如图，一艘船从A处出发，以每小时10海里的速度向正北航行，从A处测得礁石C在北偏西30°方向上，如果这艘船上午8：00从A处出发，10：00到达B处，从B处测得礁石C在北偏西60°方向上，问：下列函数图象只位于第三象限的是（ ）
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
已知平行四边形ABCD，∠A=60°，AB=2a，AD=a．请计算两条对角线的长度．