题目内容
 已知?AOBC在平面直角坐标系中的位置如图所示,点A,B的坐标分别为(3,4)(7,0),求点C的坐标.
已知?AOBC在平面直角坐标系中的位置如图所示,点A,B的坐标分别为(3,4)(7,0),求点C的坐标.考点:平行四边形的性质,坐标与图形性质
专题:
分析:首先过点A作AD⊥x轴于点D,作CE⊥x轴于点E,由四边形AOBC是平行四边形,易得Rt△OAD≌Rt△BCE(HL),又由点A,B的坐标分别为(3,4)(7,0),即可得OD=BE=3,AC=OB=7,AD=CE=4,继而求得答案.
解答: 解:过点A作AD⊥x轴于点D,作CE⊥x轴于点E,
解:过点A作AD⊥x轴于点D,作CE⊥x轴于点E,
∵四边形AOBC是平行四边形,
∴AC∥OB,AC=OB,OA∥BC,OA=BC,
∴AD=CE,
在Rt△OAD和Rt△BCE中,
,
∴Rt△OAD≌Rt△BCE(HL),
∴OD=BE,
∵点A,B的坐标分别为(3,4)(7,0),
∴OD=BE=3,AC=OB=7,AD=CE=4,
∴OE=OB+BE=10,
∴点C的坐标为:(10,4).
 解:过点A作AD⊥x轴于点D,作CE⊥x轴于点E,
解:过点A作AD⊥x轴于点D,作CE⊥x轴于点E,∵四边形AOBC是平行四边形,
∴AC∥OB,AC=OB,OA∥BC,OA=BC,
∴AD=CE,
在Rt△OAD和Rt△BCE中,
|
∴Rt△OAD≌Rt△BCE(HL),
∴OD=BE,
∵点A,B的坐标分别为(3,4)(7,0),
∴OD=BE=3,AC=OB=7,AD=CE=4,
∴OE=OB+BE=10,
∴点C的坐标为:(10,4).
点评:此题考查了平行四边形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
多项式7x2+x-1与多项式M的差是3x2-6x+5,则多项式M是( )
| A、4x2-5x+4 |
| B、10x2-5x+4 |
| C、4x2+7x-6 |
| D、-4x2-7x+6 |
 如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )
如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )| A、2cm | B、4cm |
| C、6cm | D、3cm |
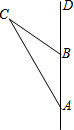 如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问:
如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问: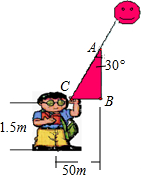 小刚家住在高层公寓的24楼,他很想知道他家离地面到底有多高.为此他在地面上进行了如图所示的测量.其中A点是小刚家,小刚身高1米五,BC距离50米.你能通过小刚的办法计算出小刚家距地面有多高吗?(请用含有根号的式子表示)
小刚家住在高层公寓的24楼,他很想知道他家离地面到底有多高.为此他在地面上进行了如图所示的测量.其中A点是小刚家,小刚身高1米五,BC距离50米.你能通过小刚的办法计算出小刚家距地面有多高吗?(请用含有根号的式子表示)