题目内容
 如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB为
如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB为考点:圆周角定理
专题:
分析:由OA=OB,可求得∠OBA=∠OAB=40°,继而求得∠AOB的度数,然后由圆周角定理,求得答案.
解答:解:∵OA=OB,
∴∠OBA=∠OAB=40°,
∴∠AOB=180°-∠OAB-∠OBA=100°,
∴∠ACB=
∠AOB=50°.
故答案为:50°.
∴∠OBA=∠OAB=40°,
∴∠AOB=180°-∠OAB-∠OBA=100°,
∴∠ACB=
| 1 |
| 2 |
故答案为:50°.
点评:此题考查了圆周角定理以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列说法正确的是( )
| A、如果a+b=0,则a=b=0 | ||
| B、如果ab=0,则a=b=0 | ||
C、如果
| ||
| D、如果|a|+|b|=0,则a=b=0 |
 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )| A、90° | B、45° |
| C、70° | D、60° |
多项式7x2+x-1与多项式M的差是3x2-6x+5,则多项式M是( )
| A、4x2-5x+4 |
| B、10x2-5x+4 |
| C、4x2+7x-6 |
| D、-4x2-7x+6 |
 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是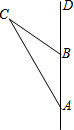 如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问:
如图,一艘船从A处出发,以每小时10海里的速度向正北航行,从A处测得礁石C在北偏西30°方向上,如果这艘船上午8:00从A处出发,10:00到达B处,从B处测得礁石C在北偏西60°方向上,问: 如图,在Rt△ABC中,斜边AB=13cm,直角边AC=5cm,以直线AB为轴旋转一周形成纺锤形,求这个纺锤形的表面积.
如图,在Rt△ABC中,斜边AB=13cm,直角边AC=5cm,以直线AB为轴旋转一周形成纺锤形,求这个纺锤形的表面积.