Question

17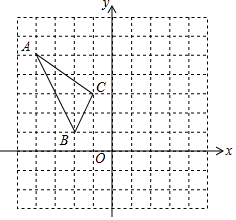．在平面直角坐标系中，每个小正方形网格的边长为单位1，格点三角形（顶点是网格线的交点的三角形）ABC如图所示．
（1）请写出点A，C的坐标；
（2）请作出三角形ABC关于y轴对称的三角形A₁B₁C₁；
（3）求△ABC中AB边上的高．

Answer 1

分析 （1）根据A、C在坐标系中的位置写出各点坐标即可；
（2）分别作出各点关于y轴的对称点，再顺次连接即可；
（3）先根据勾股定理求出AB的长，再求出△ABC的面积，进而可得出结论．

解答 解：（1）由图可知，A（-4，5），C（-1，3）； 

 （2）如图，△A₁B₁C₁即为所求； 

（3）∵AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
S_△ABC=3×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×3
=12-4-1-3
=4，
∴h=$\frac{8}{AB}$=$\frac{8}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$．

点评 本题考查的是作图-轴对称变换，熟知轴对称的性质是解答此题的关键．