题目内容
7.解下列方程组:(1)$\left\{\begin{array}{l}{2x-5y=-1}\\{2x+3y=7}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{(x+2y)-(2x-7y)=2}\end{array}\right.$.
分析 (1)直接利用加减消元法则解方程得出答案;
(2)首先整理方程组进而解方程得出答案.
解答 解:(1)$\left\{\begin{array}{l}{2x-5y=-1①}\\{2x+3y=7②}\end{array}\right.$,
②-①得:
8y=8,
解得:y=1,
故2x-5×1=-1,
解得:x=2,
故方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x+y}{2}+\frac{x-y}{3}=6}\\{(x+2y)-(2x-7y)=2}\end{array}\right.$
整理得:$\left\{\begin{array}{l}{x-9y=-2①}\\{5x+y=36②}\end{array}\right.$,
①×5-②得:
-46y=-46,
解得:y=1,
则x-9=-2,
解得:x=7,
故方程组的解为:$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$.
点评 此题主要考查了二元一次方程组的解法,正确掌握加减消元法解方程组是解题关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
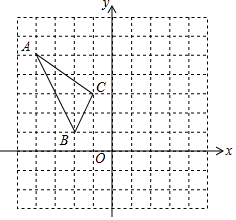 在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.
在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.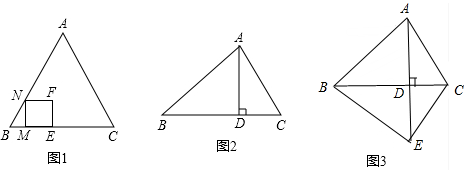
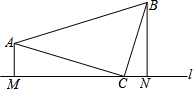 如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作过C的直线l的垂线,垂足分别为M、N.
如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作过C的直线l的垂线,垂足分别为M、N. 四边形ABCD和CEFG都是正方形(正方形的性质是四条边都相等,四个角都是直角),连结BG并延长DE于点H.
四边形ABCD和CEFG都是正方形(正方形的性质是四条边都相等,四个角都是直角),连结BG并延长DE于点H.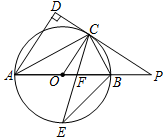 如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.