题目内容
5.是否存在这样的整数k,使得关于x、y的方程组$\left\{\begin{array}{l}{x-y=2k-1}\\{x+y=3}\end{array}\right.$的解满足$\left\{\begin{array}{l}{x>1}\\{y>0}\end{array}\right.$?若存在,请求出整数k的值;若不存在,请说明理由.分析 解关于x、y的方程组得出$\left\{\begin{array}{l}{x=k+1}\\{y=2-k}\end{array}\right.$,根据$\left\{\begin{array}{l}{x>1}\\{y>0}\end{array}\right.$知$\left\{\begin{array}{l}{k+1>1}&{①}\\{2-k>0}&{②}\end{array}\right.$,解不等式组求得k的范围即可得出答案.
解答 解:存在,
解方程组$\left\{\begin{array}{l}{x-y=2k-1}\\{x+y=3}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=k+1}\\{y=2-k}\end{array}\right.$,
∵$\left\{\begin{array}{l}{x>1}\\{y>0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k+1>1}&{①}\\{2-k>0}&{②}\end{array}\right.$,
解不等式①,得:k>0,
解不等式②,得:k<2,
则不等式的解集为0<k<2,
则整数k的值为1.
点评 本题主要考查解二元一次方程组合一元一次不等式的能力,根据题意得出关于k的不等式组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.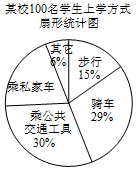 某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校100名学生上学方式频数分布表
(1)本次调查的个体是每名学生的上学方式;
(2)求频数分布表中,“乘私家车”部分对应的频数;
(3)请估计该校2 000名学生中,先把骑车和步行上学的一共有多少人?
 某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):某校100名学生上学方式频数分布表
| 方式 | 划记 | 频数 |
| 步行 | 正正正 | 15 |
| 骑车 | 正正正正正 | 29 |
| 乘公共交通工具 | 正正正正正正 | 30 |
| 乘私家车 | ||
| 其它 | ||
| 合计 | 100 |
(2)求频数分布表中,“乘私家车”部分对应的频数;
(3)请估计该校2 000名学生中,先把骑车和步行上学的一共有多少人?
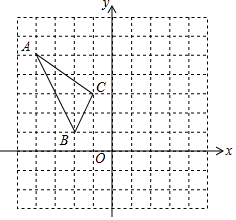 在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.
在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.