题目内容
9. 如图,在△ABC中,∠ACB=90,DE是AB的垂直平分线,∠CAE:∠EAB=4:1.
如图,在△ABC中,∠ACB=90,DE是AB的垂直平分线,∠CAE:∠EAB=4:1.(1)求∠B的度数.
(2)若AC=2,求BE.
分析 (1)根据线段垂直平分线的性质得到EA=EB,得到∠DAE=∠B,根据三角形内角和定理计算即可;
(2)根据直角三角形的性质求出AE,得到BE的长.
解答 解:(1)∵DE是AB的垂直平分线,
∴EA=EB,
∴∠DAE=∠B,
∵∠CAE:∠EAB=4:1,
∴∠B=∠DAE=15°;
(2)∵∠B=∠DAE=15°,
∴∠AEC=30°,
∴AE=2AC=4,
则BE=4.
点评 本题考查的是线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
14.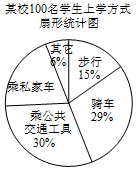 某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校100名学生上学方式频数分布表
(1)本次调查的个体是每名学生的上学方式;
(2)求频数分布表中,“乘私家车”部分对应的频数;
(3)请估计该校2 000名学生中,先把骑车和步行上学的一共有多少人?
 某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):
某校有2 000名学生.为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查.整理样本数据,得到如图表(频数分布表中部分划记被墨水盖住):某校100名学生上学方式频数分布表
| 方式 | 划记 | 频数 |
| 步行 | 正正正 | 15 |
| 骑车 | 正正正正正 | 29 |
| 乘公共交通工具 | 正正正正正正 | 30 |
| 乘私家车 | ||
| 其它 | ||
| 合计 | 100 |
(2)求频数分布表中,“乘私家车”部分对应的频数;
(3)请估计该校2 000名学生中,先把骑车和步行上学的一共有多少人?
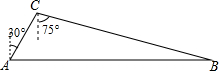 如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.
如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.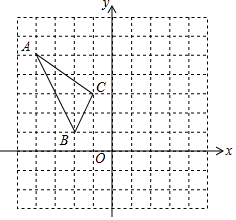 在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.
在平面直角坐标系中,每个小正方形网格的边长为单位1,格点三角形(顶点是网格线的交点的三角形)ABC如图所示.
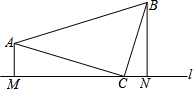 如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作过C的直线l的垂线,垂足分别为M、N.
如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作过C的直线l的垂线,垂足分别为M、N.