题目内容
19.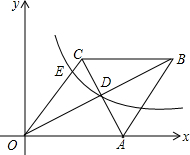 如图,在平面直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,反比例函数y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,求反比例函数的解析式.
如图,在平面直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,反比例函数y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,求反比例函数的解析式.
分析 过点C作CF⊥OA于点F,根据A(10,0)得出OC=OA=10.再由OB•AC=160,得出菱形的面积故可得出CF的长,根据勾股定理求出OF的长即可得出C点坐标,由中点坐标公式得出D点坐标,代入反比例函数的解析式即可得出k的值,进而得出结论.
解答 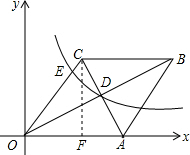 解:过点C作CF⊥OA于点F,
解:过点C作CF⊥OA于点F,
∵菱形OABC中,A(10,0),
∴OC=OA=10.
∵OB•AC=160,
∴S菱形OABC=80,
∴CF=$\frac{80}{OA}$=$\frac{80}{10}$=8,
∴OF=$\sqrt{{OC}^{2}-{CF}^{2}}$=$\sqrt{{10}^{2}-{8}^{2}}$=6,
∴C(6,8),
∴D($\frac{6+10}{2}$,$\frac{8}{2}$),即D(8,4),
∵反比例函数y=$\frac{k}{x}$(x>0)经过D点,
∴k=8×4=32,
∴反比例函数的解析式为y=$\frac{32}{x}$.
点评 本题考查的是反比例函数综合题,根据题意作出辅助线,构造出直角三角形,利用勾股定理求出CF的长,再由中点坐标公式求出D点坐标是解答此题的关键.

练习册系列答案
相关题目
10.已知a,b,c为正整数,且a2+b2+c2-ab-bc-ac=19,那么a+b+c的最小值等于( )
| A. | 11 | B. | 10 | C. | 8 | D. | 6 |
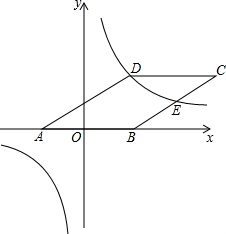 如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式.
如图,在平面直角坐标系中有一个?ABCD,其中点A(-2,0),B(2,0),C(6,4),已知反比例函数y=$\frac{k}{x}$的图象恰好经过点D,求该反比例函数的解析式.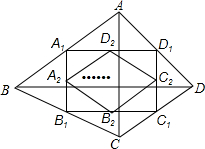 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,…,如此进行下去,得到四边形AnBnCnDn.下列结论正确的有( )