题目内容
14.已知点A(4,0),B(0,3),如果⊙A的半径为1,⊙B的半径为6,则⊙A与⊙B的位置关系是( )| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
分析 由点A(4,0),B(0,3),可求得AB的长,又由⊙A与⊙B的半径分别为:1与6,即可根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系得出两圆位置关系.
解答 解:∵点A(4,0),B,0,3),
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵⊙A与⊙B的半径分别为:1与6,
∴半径差为:6-1=5,
∴这两圆的位置关系是:内切.
故选A.
点评 此题考查了圆与圆的位置关系.注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键.

练习册系列答案
相关题目
9.一个多边形剪去一个角后(剪痕不过任何一个其它顶点),内角和为1980°,则原多边形的边数为( )
| A. | 11 | B. | 12 | C. | 13 | D. | 11或12 |
4.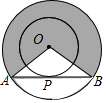 如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
 如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
 已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值.
已知,如图,∠ABC=∠BCD=90°,AC=15,sinA=$\frac{4}{5}$,BD=20,求∠D的三个三角函数值.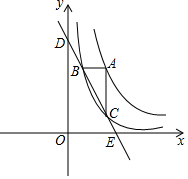 如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E.
如图,点A在函数y=$\frac{4}{x}$(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=$\frac{1}{x}$图象于点B,C,直线BC与坐标轴的交点为D,E. 小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米.
小明与班级数学兴趣小组的同学在学校操场上测得旗杆BC在地面上的影长AB为12米,同一时刻,测得小明在地面的影长为2.4米,小明的身高为1.6米. 如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.
如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,求∠B′A′C的大小.