题目内容
我们知道平行四边形那有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论
【发现与证明】
在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
结论1:B′D∥AC;
结论2:△AB′C与?ABCD重叠部分的图形是等腰三角形.
…
请利用图1证明结论1或结论2.
【应用与探究】
在?ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,连接B′D.
(1)如图1,若AB=
,∠AB′D=75°,则∠ACB= ,BC= ;
(2)如图2,AB=2
,BC=1,AB′与CD相交于点E,求△AEC的面积;
(3)已知AB=2
,当BC的长为多少时,△AB′D是直角三角形?

【发现与证明】
在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
结论1:B′D∥AC;
结论2:△AB′C与?ABCD重叠部分的图形是等腰三角形.
…
请利用图1证明结论1或结论2.
【应用与探究】
在?ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,连接B′D.
(1)如图1,若AB=
| 3 |
(2)如图2,AB=2
| 3 |
(3)已知AB=2
| 3 |

考点:几何变换综合题
专题:
分析:【发现与证明】
通过三角形全等即可求得∠ACB′=∠CAD,即可得到结论2;进而根据等腰三角形的性质证得∠ADB′=∠DAC,根据平行线的判定即可证得结论1;
【应用与探究】
(1)根据对折的性质求得∠AB′C=30°,从而求得∠CB′D=45°,由于B′D∥AC,得出∠ACB′=∠CB′D=45°,进而即可求得∠ACB=45°;作AG⊥BC于G,根据解直角三角形即可求得BC;
(2)作CG⊥AB′于G,通过解直角三角形求得CG=
,B′G=
,进而求得AG=2
-
=
,设AE=CE=x,则EG=
-x,根据勾股定理即可求得x值,即AE的值,然后根据三角形的面积公式即可求得△AEC的面积;
(3)先证得四边形ACB′D是等腰梯形,根据等腰梯形的性质得出∠AB′C=∠CDA=30°,∠B′AD=∠DCB′=90°,设∠ADB′=∠CB′D=y,则∠AB′D=y-30°,根据∠AB′D+∠ADB′=90°,得出y-30°+y=90°,解得y=60°,进而求得∠AB′D=30°,通过解直角三角形即可求得BC.
通过三角形全等即可求得∠ACB′=∠CAD,即可得到结论2;进而根据等腰三角形的性质证得∠ADB′=∠DAC,根据平行线的判定即可证得结论1;
【应用与探究】
(1)根据对折的性质求得∠AB′C=30°,从而求得∠CB′D=45°,由于B′D∥AC,得出∠ACB′=∠CB′D=45°,进而即可求得∠ACB=45°;作AG⊥BC于G,根据解直角三角形即可求得BC;
(2)作CG⊥AB′于G,通过解直角三角形求得CG=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
(3)先证得四边形ACB′D是等腰梯形,根据等腰梯形的性质得出∠AB′C=∠CDA=30°,∠B′AD=∠DCB′=90°,设∠ADB′=∠CB′D=y,则∠AB′D=y-30°,根据∠AB′D+∠ADB′=90°,得出y-30°+y=90°,解得y=60°,进而求得∠AB′D=30°,通过解直角三角形即可求得BC.
解答: 解:【发现与证明】
解:【发现与证明】
在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
如图1,∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠ADC,
∵将△ABC沿AC翻折至△AB′C,
∴AB′=AB,B′C=BC,∠AB′C=∠B,
∴AB′=CD,B′C=AD,∠AB′C=∠ADC,
在△AB′C和△CAD中,
,
∴△AB′C≌△CAD(SAS),
∴∠ACB′=∠CAD,
设AD、B′C相交于E,
∴AE=CE,
∴△ACE是等腰三角形,
即△AB′C与?ABCD重叠部分的图形是等腰三角形;
∵B′C=AD,AE=CE,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
【应用与探究】
(1)如图1,∵在?ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,
∴∠AB′C=30°,
∵∠AB′D=75°,
∴∠CB′D=45°,
∵B′D∥AC,
∴∠ACB′=∠CB′D=45°,
∵∠ACB=∠ACB′,
∴∠ACB=45°;
作AG⊥BC于G,
∴AG=CG,
∵∠B=30°,
∴AG=
AB=
×
=
,
∴CG=
,BG=
=
,
∴BC=BG+CG=
,
故答案为:45°,
;
(2)如图2,
作CG⊥AB′于G,
∵∠B=30°,
∴∠AB′C=30°,
∴CG=
B′C=
BC=
,B′G=
B′C=
BC=
,
∵AB′=AB=2
,
∴AG=2
-
=
,
设AE=CE=x,则EG=
-x,
∵CG2+EG2=CE2,
∴(
)2+(
-x)2=x2,解得x=
,
∴AE=
,
∴△AEC的面积=
AE•CG=
×
×
=
;
(3)如图2,∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠B=30°,
∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
当∠B′AD=90°,AB>BC时,
设∠ADB′=∠CB′D=y,
∴∠AB′D=y-30°,
∵∠AB′D+∠ADB′=90°,
∴y-30°+y=90°,解得y=60°,
∴∠AB′D=y-30°=30°,
∵AB′=AB=2
,
∴AD=
×2
=2,
∴BC=2,
当∠ADB′=90°,AB>BC时,如图3,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=2
,
∴BC=
AB=
×2
=3;
当∠B′AD=90°AB<BC时,如图4,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2
,
∴∠AB′C=30°,
∴GC=
B′C=
BC,
∴G是BC的中点,
在RT△ABG中,BG=
AB=
×2
=3,
∴BC=6;
当∠AB′D=90°时,如图5,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2
,
∴BC=AB÷
=2
×
=4;
∴已知当BC的长为2或3或4或6时,△AB′D是直角三角形.
 解:【发现与证明】
解:【发现与证明】在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
如图1,∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠ADC,
∵将△ABC沿AC翻折至△AB′C,
∴AB′=AB,B′C=BC,∠AB′C=∠B,
∴AB′=CD,B′C=AD,∠AB′C=∠ADC,
在△AB′C和△CAD中,
|
∴△AB′C≌△CAD(SAS),
∴∠ACB′=∠CAD,
设AD、B′C相交于E,
∴AE=CE,
∴△ACE是等腰三角形,
即△AB′C与?ABCD重叠部分的图形是等腰三角形;
∵B′C=AD,AE=CE,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
【应用与探究】
(1)如图1,∵在?ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,
∴∠AB′C=30°,
∵∠AB′D=75°,
∴∠CB′D=45°,
∵B′D∥AC,
∴∠ACB′=∠CB′D=45°,
∵∠ACB=∠ACB′,
∴∠ACB=45°;
作AG⊥BC于G,
∴AG=CG,
∵∠B=30°,
∴AG=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴CG=
| ||
| 2 |
| AB2-AG2 |
| 3 |
| 2 |
∴BC=BG+CG=
3+
| ||
| 2 |
故答案为:45°,
3+
| ||
| 2 |
(2)如图2,

作CG⊥AB′于G,
∵∠B=30°,
∴∠AB′C=30°,
∴CG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵AB′=AB=2
| 3 |
∴AG=2
| 3 |
| ||
| 2 |
3
| ||
| 2 |
设AE=CE=x,则EG=
3
| ||
| 2 |
∵CG2+EG2=CE2,
∴(
| 1 |
| 2 |
3
| ||
| 2 |
7
| ||
| 9 |
∴AE=
7
| ||
| 9 |
∴△AEC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
7
| ||
| 9 |
| 1 |
| 2 |
7
| ||
| 36 |
(3)如图2,∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠B=30°,
∴∠AB′C=∠CDA=30°,
∵△AB′D是直角三角形,
当∠B′AD=90°,AB>BC时,
设∠ADB′=∠CB′D=y,
∴∠AB′D=y-30°,
∵∠AB′D+∠ADB′=90°,
∴y-30°+y=90°,解得y=60°,
∴∠AB′D=y-30°=30°,
∵AB′=AB=2
| 3 |
∴AD=
| ||
| 3 |
| 3 |
∴BC=2,
当∠ADB′=90°,AB>BC时,如图3,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACB′D是等腰梯形,
∵∠ADB′=90°,
∴四边形ACB′D是矩形,
∴∠ACB′=90°,
∴∠ACB=90°,
∵∠B=30°,AB=2
| 3 |
∴BC=
| ||
| 2 |
| ||
| 2 |
| 3 |
当∠B′AD=90°AB<BC时,如图4,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2
| 3 |
∴∠AB′C=30°,
∴GC=
| 1 |
| 2 |
| 1 |
| 2 |
∴G是BC的中点,
在RT△ABG中,BG=
| ||
| 2 |
| ||
| 2 |
| 3 |
∴BC=6;
当∠AB′D=90°时,如图5,

∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2
| 3 |
∴BC=AB÷
| ||
| 2 |
| 3 |
| 1 | ||||
|
∴已知当BC的长为2或3或4或6时,△AB′D是直角三角形.
点评:本题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )| A、AB=AC |
| B、∠BAD=∠CAE |
| C、BD=CE |
| D、AD=DE |
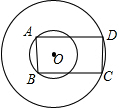 如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为
如图,两同心圆的半径分别为6、10,矩形ABCD的边AB、CD分别为两圆的弦.当矩形面积取最大值时,其周长为