题目内容

如图，⊙O的直径AB⊥弦CD，且∠BAC=40°，则∠BOD的度数为（　　）
A、20°B、30°
C、40°D、80°
考点：圆周角定理,垂径定理
专题：
分析：连接OC，先由垂径定理得到
BC
=
BD
，然后由圆周角定理求出∠BOC的度数，再根据等弧所对的圆心角相等即可得出结论．
解答：解：连接OC，

∵⊙O的直径AB⊥弦CD，
∴
BC
=
BD
，
∵∠BAC=40°，
∴∠BOC=2∠BAC=80°；
∵
BC
=
BD
，
∴∠BOD=∠BOC=80°．
故选D．
点评：本题考查的是圆周角定理的应用．解题时，通过辅助线OC，构造了同弧所对的圆周角∠A和圆心角∠COB，从而使隐藏在题设中的圆周角定理显现出来．
练习册系列答案
相关题目
如图，在平面直角坐标系中，点A的坐标是（5，0），点P是直线BCy=-x+6上的一动点：
（1）求B点和C点的坐标；
（2）求当点P运动到与y轴的距离是4时的△OPA的面积；
（3）在直线BC上是否存在点P，是S△OBP=
1
2
S△OBC？若存在，请求出P点的坐标；若不存在请说明理由．
在Rt△ABC中，∠C=90°，a，b，c分别是∠A，∠B，∠C的对边，则
a
c
等于（　　）
A、sinBB、cosA
C、cosBD、tanB
如图，一个三角板的直角顶点在直线l上，∠1=25°，那么∠2为（　　）
A、25°B、45°
C、55°D、65°
下列各组图形中相似的图形是（　　）
A、对应边成比例的多边形
B、四个角都对应相等的两个梯形
C、有一个角相等的两个菱形
D、各边对应成比例的两个平行四边形
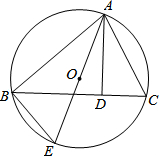如图，AE是△ABC外接圆O的直径，连结BE，作AD⊥BC于D．
（1）求证：△ABE∽△ADC；
（2）若AB=8，AC=6，AE=10，求AD的长．
如图，斜坡AC的坡度（坡高比水平距离）为1：
3
，AC=10米．坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB=14米．旗杆BC的高度是
 
．
函数y=
x+1
中，自变量x的取值范围是（　　）
A、x≥-1B、x＞-1
C、x≥0D、x≠0
m3-4m=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网