题目内容
平面上有6条两两不平行的直线，求证：在所有的交角中，至少有一个角小于30.1°．
考点：反证法
专题：证明题
分析：首先假设所有的角都大于等于30.1°，进而得出矛盾，从而得出原命题成立．
解答：证明：假设所有的角都大于等于30.1°，
1、假设6条线相交于同一点p，则以点p为中心形成12个角．如果所有的角都≥30.1°，
则其和≥361.2＞360，与圆心角=360度矛盾．
2、假设6条线不相交于同一点．则可通过平移，使6条线相交于同一点，角的度数不变，通过1的结论，可知与定理矛盾．
综上可知假设不成立，因此至少有一个角小于30.1°．
1、假设6条线相交于同一点p，则以点p为中心形成12个角．如果所有的角都≥30.1°，
则其和≥361.2＞360，与圆心角=360度矛盾．
2、假设6条线不相交于同一点．则可通过平移，使6条线相交于同一点，角的度数不变，通过1的结论，可知与定理矛盾．
综上可知假设不成立，因此至少有一个角小于30.1°．
点评：此题主要考查了反证法，正确利用反证法的步骤，从结论的反面出发得出矛盾进而证明是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
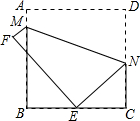如图，将一张边长为8的正方形纸片ABCD折叠，使点D落在BC的中点E处，点A落在点F处，折痕为MN，则线段MN的长为（ ）| A、10 | ||
B、4
| ||
C、
| ||
D、2
|
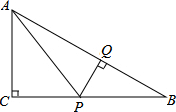在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．
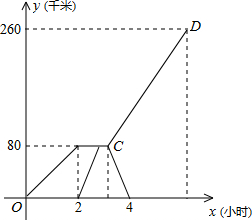已知，A、B两市相距260千米，甲车从A市前往B市运送物资，行驶2小时在M地汽车出现故障，立即通知技术人员乘乙车从A市赶来维修（通知时间忽略不计），乙车到达M地后又经过20分钟修好甲车后以原速原路返回，同时甲车以原速1.5倍的速度前往B市，如图是两车距A市的路程y（千米）与甲车行驶时间x（小时）之间的函数图象，结合图象回答下列问题：
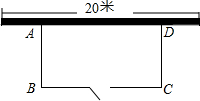某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地，如图，墙长20米，BC边有一个宽为1米的木门（木门用其它材料做不点用竹篱笆）．设养鸡场AB边的长为x米，BC边的长为y米，BC的长度不小于10米且不超过墙长．求y关于x的函数解析式及x的取值范围．
如图，在△ABC中，∠BAC的角平分线AD交BC于E，交△ABC的外接圆⊙O于D．
如图，在平面直角坐标系中，点O为坐标系原点，矩形OABC的边OA，OC分别在x轴和y轴上，其中OA=6，OC=3．已知反比例函数y=