题目内容
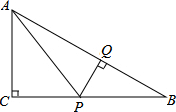 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值;
(3)在Rt△ABC中,两条直角边BC、AC满足关系式BC=λAC,是否存在一个λ的值,使Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等.
考点:相似形综合题,二次函数的最值,三角形的面积,全等三角形的性质
专题:几何综合题
分析:(1)利用“两角法”可以证得△PBQ与△ABC相似;
(2)设BP=x(0<x<4).由勾股定理、(1)中相似三角形的对应边成比例以及三角形的面积公式列出S与x的函数关系式,利用配方法求得二次函数的最值;
(3)利用全等三角形的对应边相等得到AQ=AC,AQ=QB,即AQ=QB=AC.在Rt△ABC中,由勾股定理得 BC2=AB2-AC2,易求得:BC=
AC,则λ=
.
(2)设BP=x(0<x<4).由勾股定理、(1)中相似三角形的对应边成比例以及三角形的面积公式列出S与x的函数关系式,利用配方法求得二次函数的最值;
(3)利用全等三角形的对应边相等得到AQ=AC,AQ=QB,即AQ=QB=AC.在Rt△ABC中,由勾股定理得 BC2=AB2-AC2,易求得:BC=
| 3 |
| 3 |
解答: 解:(1)不论点P在BC边上何处时,都有
解:(1)不论点P在BC边上何处时,都有
∠PQB=∠C=90°,∠B=∠B
∴△PBQ∽△ABC;
(2)设BP=x(0<x<4),由勾股定理,得 AB=5
∵由(1)知,△PBQ∽△ABC,
∴
=
=
,即
=
=
∴PQ=
x,QB=
x
S△APQ=
PQ×AQ
=-
x2+
x
=-
(x-
)2+
∴当x=
时,△APQ的面积最大,最大值是
;
(3)存在.
∵Rt△AQP≌Rt△ACP
∴AQ=AC
又∵Rt△AQP≌Rt△BQP
∴AQ=QB
∴AQ=QB=AC
在Rt△ABC中,由勾股定理得 BC2=AB2-AC2
∴BC=
AC
∴λ=
时,Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等.
 解:(1)不论点P在BC边上何处时,都有
解:(1)不论点P在BC边上何处时,都有∠PQB=∠C=90°,∠B=∠B
∴△PBQ∽△ABC;
(2)设BP=x(0<x<4),由勾股定理,得 AB=5
∵由(1)知,△PBQ∽△ABC,
∴
| PQ |
| AC |
| QB |
| BC |
| PB |
| AB |
| PQ |
| 3 |
| QB |
| 4 |
| x |
| 5 |
∴PQ=
| 3 |
| 5 |
| 4 |
| 5 |
S△APQ=
| 1 |
| 2 |
=-
| 6 |
| 25 |
| 3 |
| 2 |
=-
| 6 |
| 25 |
| 25 |
| 8 |
| 75 |
| 32 |
∴当x=
| 25 |
| 8 |
| 75 |
| 32 |
(3)存在.
∵Rt△AQP≌Rt△ACP
∴AQ=AC
又∵Rt△AQP≌Rt△BQP
∴AQ=QB
∴AQ=QB=AC
在Rt△ABC中,由勾股定理得 BC2=AB2-AC2
∴BC=
| 3 |
∴λ=
| 3 |
点评:本题综合考查了相似三角形的判定与性质,全等三角形的性质,三角形的面积公式以及二次函数的最值的求法等知识点.难度较大.注意,在证明三角形相似时,充分利用公共角,在利用全等三角形的性质时,要找准对应边.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知点P(2-a,3a+6)在第四象限,且到两坐标轴的距离相等,则P点的坐标为( )
| A、(2,-2) |
| B、(3,-3) |
| C、(4,-4) |
| D、(6,-6) |
把分式
中x、y都扩大2倍,则分式的值( )
| x+y |
| 3x |
| A、扩大4倍 | B、扩大2倍 |
| C、缩小2倍 | D、不变 |
 如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.
如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC. 如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?