题目内容
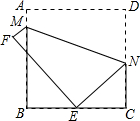 如图,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,则线段MN的长为( )
如图,将一张边长为8的正方形纸片ABCD折叠,使点D落在BC的中点E处,点A落在点F处,折痕为MN,则线段MN的长为( )| A、10 | ||
B、4
| ||
C、
| ||
D、2
|
考点:翻折变换(折叠问题)
专题:
分析:连接ME,作MP⊥CD交CD于点P,根据折叠的性质,在RT△ECM中,若根据勾股定理就可以列出方程,从而解出CN的长.在RT△MFE中,有MF2+FE2=ME2,在RT△MBE中,有BE2+BM2=ME2,根据这两个式子可求得MF=1,得到AM=PD=1,NP=4,在RT△MPN中,运用勾股定理求出MN=4
.
| 5 |
解答:
解:如图,连接ME,作MP⊥CD交CD于点P,
由四边形ABCD是正方形及折叠性知,AM=MF,EN=DF,EF=AD,∠MFE=∠BAD=90°,
在RT△ECM中,CE2+CN2=EN2,
∵AB=BC=CD=DA=8,E为BC的中点
∴CE=4,
∴42+CN2=(8-CN)2
解得CN=3,
在RT△MFE中,MF2+FE2=ME2,
在RT△MBE中,BE2+BM2=ME2,
∴MF2+FE2=BE2+BM2,
∴MF2+82=42+(8-MF)2
解得,MF=1,
∴AM=PD=1,
∴NP=CD-CN-PD=8-3-1=4,
在RT△MPN中,
MN=
=
=4
故选:B.

解:如图,连接ME,作MP⊥CD交CD于点P,
由四边形ABCD是正方形及折叠性知,AM=MF,EN=DF,EF=AD,∠MFE=∠BAD=90°,
在RT△ECM中,CE2+CN2=EN2,
∵AB=BC=CD=DA=8,E为BC的中点
∴CE=4,
∴42+CN2=(8-CN)2
解得CN=3,
在RT△MFE中,MF2+FE2=ME2,
在RT△MBE中,BE2+BM2=ME2,
∴MF2+FE2=BE2+BM2,
∴MF2+82=42+(8-MF)2
解得,MF=1,
∴AM=PD=1,
∴NP=CD-CN-PD=8-3-1=4,
在RT△MPN中,
MN=
| MP2+PN2 |
| 82+42 |
| 5 |
故选:B.
点评:本题考查翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相应的直角三角形利用勾股定理求解是解决本题的关键.

练习册系列答案
相关题目
已知点P(2-a,3a+6)在第四象限,且到两坐标轴的距离相等,则P点的坐标为( )
| A、(2,-2) |
| B、(3,-3) |
| C、(4,-4) |
| D、(6,-6) |
下列各式:
(1-x),
,
,
,
,其中分式共有( )
| 1 |
| 5 |
| 4x |
| π-3 |
| x2-y2 |
| 2 |
| 1+a |
| b |
| 5x2 |
| y |
| A、2个 | B、3个 | C、4个 | D、5个 |
若二次根式
在实数范围内有意义,则x的取值范围是( )
| 6-3x |
| A、x≤2 | B、x≥2 |
| C、x<2 | D、x≠2 |
2的相反数是( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
把分式
中x、y都扩大2倍,则分式的值( )
| x+y |
| 3x |
| A、扩大4倍 | B、扩大2倍 |
| C、缩小2倍 | D、不变 |
 一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发
一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发