题目内容
16.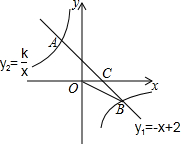 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.(1)求反比例函数的解析式;
(2)当y1<y2时,求x的取值范围.
分析 (1)作BD⊥x轴于D,如图,在Rt△OBD中,根据正切的定义得到tan∠BOC=$\frac{BD}{OD}$=$\frac{1}{2}$,则$\frac{-n}{m}$=$\frac{1}{2}$,即m=-2n,再把点B(m,n)代入y1=-x+2得n=-m+2,然后解关于m、n的方程组得到n=-2,m=4,即B点坐标为(4,-2),再把B(4,-2)代入y2=$\frac{k}{x}$可计算出k=-8,所以反比例函数解析式为y2=-$\frac{8}{x}$;
(2)根据函数图象即可得.
解答 解:(1)作BD⊥x轴于D,如图,
在Rt△OBD中,tan∠BOC=$\frac{BD}{OD}$=$\frac{1}{2}$,
设点B坐标为(m,n),
∴$\frac{-n}{m}$=$\frac{1}{2}$,即m=-2n,
把点B(m,n)代入y1=-x+2得n=-m+2,
∴n=2n+2,解得n=-2,
∴m=4,
∴B点坐标为(4,-2),
把B(4,-2)代入y2=$\frac{k}{x}$得k=4×(-2)=-8,
∴反比例函数解析式为y2=-$\frac{8}{x}$;
(2)由函数图象可得,-2<x<0或x>4时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
1.下列方程中,变形正确的是( )
| A. | 若$\frac{1}{2}$x=x-1,则x=2x-1 | B. | 若$\frac{1}{3}$x=2,则x=$\frac{2}{3}$ | ||
| C. | 若3x-1=x+2,则3x-x=2+1 | D. | 若2(x-2)=5,则2x=5-4 |
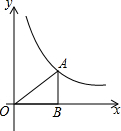 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB⊥x轴于点B,则△ABO的面积为2.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB⊥x轴于点B,则△ABO的面积为2. 如图,AB是⊙O的直径,点D在⊙O上,OC⊥AD,垂足为F,与⊙O交于点E,且∠C=∠BED.
如图,AB是⊙O的直径,点D在⊙O上,OC⊥AD,垂足为F,与⊙O交于点E,且∠C=∠BED.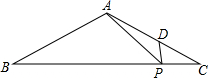 已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,
已知:如图,在△ABC中,AB=AC=13,BC=24,点P、D分别在边BC、AC上,AP2=AD•AB,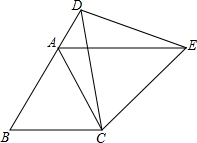 如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边△CDE,连接AE.
如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边△CDE,连接AE.