题目内容
8.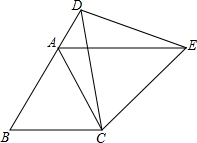 如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边△CDE,连接AE.
如图,△ABC为等边三角形,D为边BA延长线上一点,连接CD,以CD为一边作等边△CDE,连接AE.(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
分析 (1)只要证明∠ACE=∠BCD,根据SAS即可证明.
(2)结论:AE∥BC.只要证明∠CAE=∠ACB=60°即可.
解答 (1)证明:∵△ABC,△DCE为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=∠B=60°,
∴∠ACE=∠BCD,
在∠ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{EC=DC}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
(2)解:结论:AE∥BC.
理由:∵△ACE≌△BCD,
∴∠EAC=∠DBC=60°,
∵∠ACB=∠DBC=60°,
∴∠EAC=∠ACB=60°,
∴AE∥BC.
点评 本题考查等边三角形的性质、全等三角形的判定和性质、平行线的判定等知识,解题的关键是正确寻找全等三角形,学会利用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.我国最新研制的巨型计算机“曙光3000超级服务器”,它的运算峰值可以达到每秒403200000000次.这个数字用科学记数法来表示( )
| A. | 4032×108 | B. | 4.032×1010 | C. | 4.032×1011 | D. | 4.032×1012 |
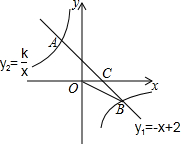 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.