题目内容
4. 如图,AB是⊙O的直径,点D在⊙O上,OC⊥AD,垂足为F,与⊙O交于点E,且∠C=∠BED.
如图,AB是⊙O的直径,点D在⊙O上,OC⊥AD,垂足为F,与⊙O交于点E,且∠C=∠BED.(1)判断AC与⊙O的位置关系,并说明理由;
(2)若OA=10,AD=16,求AC的长.
分析 (1)由圆周角定理与∠C=∠BED,易得∠C=∠BAD,又由OC⊥AD,易得∠OAC=90°,即可证得AC是⊙O的切线;
(2)由AB是⊙O的直径,可得∠ADB=90°,继而可证得△ABD∽△COA,然后由相似三角形的对应边成比例,求得答案.
解答 解:(1)AC与⊙O相切.
理由:∵∠C=∠BED,∠BAD=∠BED,
∴∠C=∠BAD,
∵OC⊥AD,
∴∠C+∠CAF=90°,
∴∠BAD+∠CAF=90°,
∴∠OAC=90°,
即OA⊥AC,
∴AC是⊙O的切线;
(2)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠ADB=∠OAC,
∵OA=10,AD=16,
∴AB=2OA=20,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=12,
∵∠C=∠BAD,
∴△ABD∽△COA,
∴AD:AC=BD:OA,
∴$\frac{16}{AC}=\frac{12}{10}$,
解:AC=$\frac{40}{3}$.
点评 此题考查了切线的判定、圆周角的性质以及相似三角形的判定与性质.注意判定切线的关键是证得∠OAC=90°,求AC长的关键是证得△ABD∽△COA.

练习册系列答案
相关题目
15.抛物线y=x2-1的顶点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
13.我国最新研制的巨型计算机“曙光3000超级服务器”,它的运算峰值可以达到每秒403200000000次.这个数字用科学记数法来表示( )
| A. | 4032×108 | B. | 4.032×1010 | C. | 4.032×1011 | D. | 4.032×1012 |
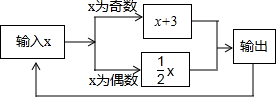 有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2017次输出的结果是1.
有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2017次输出的结果是1.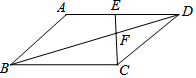 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△EDF:S△BFC:S△BCD等于1:4:6.
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则S△EDF:S△BFC:S△BCD等于1:4:6.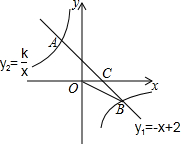 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$. 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.