题目内容

18．如果梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，AD=1，BC=3，那么四边形AEFD与四边形EBCF的面积比是3：5．

分析 直接利用梯形的中位线定理得出EF的长度，再利用梯形面积公式解答即可．

解答 解：∵梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，
∴EF=2，
设梯形ABCD的高为2h，
可得四边形AEFD与四边形EBCF的面积比=$\frac{1}{2}（1+2）h：\frac{1}{2}（2+3）h$=3：5；
故答案为：3：5．

点评 此题考查梯形中位线问题，关键是知道梯形中位线平行梯形上下底且等于上下底的和的一半．

练习册系列答案
相关题目
8．△ABC的一边长为5，另两边分别是方程x2-6x+m=0的两根，则m的取值范围是（　　）
A．m＞$\frac{11}{4}$B．$\frac{11}{4}$＜m≤9C．$\frac{11}{4}$≤m≤9D．m≤$\frac{11}{4}$
9．小军家的玩具店进了一箱除颜色外都相同的塑料球共1000个，小军将箱中的球搅匀后，随机摸出一个球记下颜色，放回箱中；搅匀后再随机摸出一个球记下颜色，放回箱中；…多次重复上述实验后，发现摸到红球的频率逐渐稳定在0.2，由此可以估计纸箱内红球的个数约是200个．
6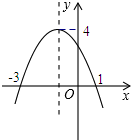．若二次函数y=ax2+bx+c（a＜0）的图象如图所示，且关于x的方程ax2+bx+c=k有两个不相等的实根，则常数k的取值范围是（　　）
A．0＜k＜4B．-3＜k＜1C．k＜-3或k＞1D．k＜4
13．把一批图书分给某班同学阅读，如果每人分4本，则余30本，如果每人分5本，则缺20本，设这个班有x名同学，y本图书，得方程组$\left\{\begin{array}{l}{4x+30=y}\\{5x-20=y}\end{array}\right.$．
3．在北京，乘坐地铁是市民出行时经常采用的一种交通方式，据调查，新票改革政策的实施给北京市轨道交通客流带来很大变化．根据2015年1月公布的调价后市民当时乘坐地铁的相关调查数据，制作了一下统计表以及统计图．

根据以上信息解答下列问题：
（1）补全扇形图；
（2）题目所给出的线路中，调价后客流量下降百分比最高的线路是2号线，调价后里程x（千米）在52＜x≤72范围内的客流量下降最明显．对于表中客流量不降反增而且增长率最高的线路，如果继续按此变化率增长，预计2016年1月这条线路的日均客流量将达到22.2万人次（精确到0.1）
（3）小王同学上学时，需要乘坐地铁15.9公里到达学校，每天上下学共乘坐两次．问调价后小王每周（按5天计算）乘坐地铁的费用比调价前多支出30元．（不考虑使用一卡通刷卡优惠，调价前每次乘坐地铁票价为2元）
10．解下列方程组：
（1）$\left\{\begin{array}{l}{y=2x-1}\\{3x+2y=5}\end{array}\right.$ 
（2）$\left\{\begin{array}{l}{4（x+y）-5（x-y）=-2}\\{\frac{2x-y}{3}-\frac{x+y}{2}=1}\end{array}\right.$．
7．阅读材料：解方程组$\left\{\begin{array}{l}{x-y-1=0①}\\{4（x-y）-y=5②}\end{array}\right.$时，可由①得x-y=1③，然后再将③代入②得4×1-y=5，求得y=-1，从而进一步求得$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$．这种方法被称为“整体代入法”．
请用上述方法解方程组：$\left\{\begin{array}{l}{6x-2y=3}\\{（3x-y）（3x+4y）=6}\end{array}\right.$．
8．下列各式中，属于最简二次根式的是（　　）
A．$\sqrt{4}$B．$\sqrt{\frac{1}{5}}$C．$\sqrt{6}$D．$\sqrt{8}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网