题目内容
8．已知a2-4a+1=0，求：（1）a2+$\frac{1}{{a}^{2}}$的值；（2）a4+$\frac{1}{{a}^{4}}$的值．分析 （1）把方程两边除以a，即可求出a+$\frac{1}{a}$=4，再根据完全平方公式进行变形，即可求出答案；
（2）根据公式得出a4+$\frac{1}{{a}^{4}}$=（a2+$\frac{1}{{a}^{2}}$）2-2•a2•$\frac{1}{{a}^{2}}$，再代入求出即可．
解答 解：（1）∵a2-4a+1=0，
∴两边除以a得：a-4+$\frac{1}{a}$=0，
a+$\frac{1}{a}$=4，
∴a2+$\frac{1}{{a}^{2}}$=（a+$\frac{1}{a}$）2-2•a•$\frac{1}{a}$=42-2=14；
（2）∵a2+$\frac{1}{{a}^{2}}$=14，
∴a4+$\frac{1}{{a}^{4}}$=（a2+$\frac{1}{{a}^{2}}$）2-2•a2•$\frac{1}{{a}^{2}}$=142-2=194．
点评 本题考查了完全平方公式的应用，能灵活运用公式进行变形是解此题的关键．
练习册系列答案
相关题目
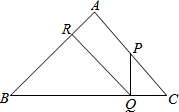如图，已知：在△ABC中，∠A=90°，AB=AC=1，P是AC上不与A、C重合的一动点，PQ⊥BC于Q，QR⊥AB于R．
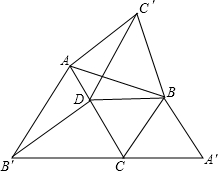如图，△ABC中，∠ACB=60°，△ABC′，△BCA′，△CAB′都是△ABC形外的等边三角形，点D在边AC 上，且DC=BC．连接DB，DB′，DC′．有下列结论：
如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，设运动的时间为ts（0＜t＜6），试尝试探究下列问题：
