题目内容
17.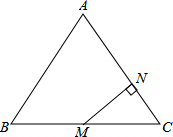 如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,
如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,①连接AM,则AM与BC是什么位置关系?证明你的结论;
②求MN的长.
分析 (1)利用等腰△ABC“三合一”的性质推知AM与BC垂直;
(2)利用等腰△ABC“三合一”的性质推知BM=CM=$\frac{1}{2}$BC=3.然后在直角Rt△ABM中,由勾股定理得AM=4;最后利用△AMC的面积的求法来求MN的长度.
解答 解:(1)AM与BC是垂直关系,理由如下:
∵AB=AC,
∵M为BC中点,
∴AM⊥BC;
(2)∵AB=AC,AM为BC的中线,
∴AM⊥BC,BM=CM=$\frac{1}{2}$BC=3.
Rt△ABM中,由勾股定理得AM=4,
S△AMC=$\frac{1}{2}$AM×MC=$\frac{1}{2}$AC×MN=6,
∴MN=$\frac{12}{5}$.
点评 本题考查了勾股定理、等腰三角形的性质.解答该题的关键是利用等腰三角形的“三合一”的性质求得BM的长度.

练习册系列答案
相关题目
9.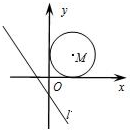 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )| A. | 2.5 | B. | 5-2$\sqrt{2}$ | C. | 2.5或10 | D. | 5-2$\sqrt{2}$或5+2$\sqrt{2}$ |
6.某商场三月份销售某品牌电视机,统计了其中三种型号电视机的销售量如下表显示:
根据本月各种型号电视机的销售全额和各种型号电视机的单价(销售全额=销售量×单价),制作了如下所示的统计图
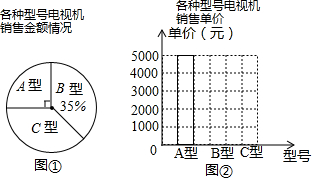
由图解答下列问题:
(1)求该商场三月份销售这三种型号电视机的总销售金额;
(2)求出B,C两种型号电视机的销售单价,并把图②中的条形统计图补充完整;
(3)四月份,该商场三种电视机的销售单价不变,三种型号电视机共销出35台,已知A,B,C三种型号电视机销售数量的中位数是15台,总销售金额为98500元,求A,B,C三种型号电视机在四月份各销售了多少台?
| 电视机型号 | A型 | B型 | C型 |
| 销售量(台) | 5 | 10 | 20 |

由图解答下列问题:
(1)求该商场三月份销售这三种型号电视机的总销售金额;
(2)求出B,C两种型号电视机的销售单价,并把图②中的条形统计图补充完整;
(3)四月份,该商场三种电视机的销售单价不变,三种型号电视机共销出35台,已知A,B,C三种型号电视机销售数量的中位数是15台,总销售金额为98500元,求A,B,C三种型号电视机在四月份各销售了多少台?
7.下列运算正确的是( )
| A. | 2x2÷x2=2x | B. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 | C. | 3x2+2x2=5x2 | D. | (x-3)2=x2-9 |
 已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.
已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.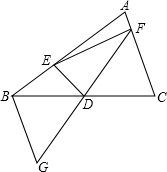 如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.
如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.
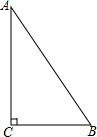 已知,如图所示,在Rt△ABC中,∠C=90°,
已知,如图所示,在Rt△ABC中,∠C=90°,