题目内容
19. 已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.
已知抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点A,点A在第一象限内且满足b=2t,设OA与x轴正方向的夹角为α,求tanα的取值范围.(注:tanA=$\frac{BC}{AC}$)
分析 根据抛物线与直线只有一个交点和b=2t,用t表示a,求出点A的坐标,根据锐角三角函数的概念表示出tanα,确定tanα的取值范围.
解答 解:∵b=2t,∴y=x2+ax+2t,
联立y=x+t得:x2+(a-1)x+t=0,
∵抛物线y=-x2+ax+b与直线y=x+t有且只有一个交点,
∴△=(a-1)2-4t=0,
∴(a-1)2=4t,(t≥0)
解得:a=1±2$\sqrt{t}$,
∴x=$\frac{-(a-1)}{2}$=±$\sqrt{t}$,
∵点A在第一象限,∴x=$\sqrt{t}$,y=$\sqrt{t}$+t,
tanα=$\frac{y}{x}$=$\frac{\sqrt{t}+t}{\sqrt{t}}$=$\sqrt{t}$+1≥1,
∴tanα≥1.
点评 本题考查的是二次函数的性质、抛物线与直线的交点坐标的求法和锐角三角函数的概念,灵活运用所学的知识是解题的关键,解答此类题目时,要认真审题,大胆计算.

练习册系列答案
相关题目
9.下列各组数据中,能构成三角形的是( )
| A. | 2cm,2cm,4cm | B. | 3cm,3cm,4cm | C. | 4cm,9cm,3cm | D. | 2cm,1cm,5cm |
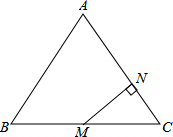 如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,
如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,