题目内容
8.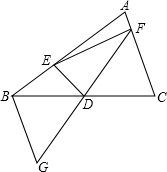 如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.
如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.(1)求证:BG=CF;
(2)DE⊥GF交AB于点E,连接EF,试判断BE+CF与EF的大小,并证明你的结论.
分析 (1)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;
(2)再利用全等的性质可得GD=FD,再有DE⊥GF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
解答 (1)证明:∵BG∥AC,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
在△BGD与△CFD中,$\left\{\begin{array}{l}{∠DBG=∠DCF}\\{BD=CD}\\{∠BDG=∠CDF}\end{array}\right.$
∴△BGD≌△CFD(ASA).
∴BG=CF.
(2)解:BE+CF>EF.
连接EG,
∵△BGD≌△CFD,
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

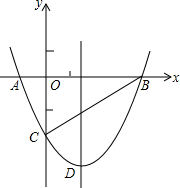 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).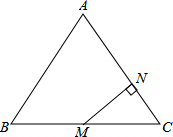 如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,
如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,