题目内容

2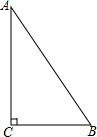．已知，如图所示，在Rt△ABC中，∠C=90°，
（1）作∠B的平分线BD交AC于点D；（要求：尺规作图，保留作图痕迹，不写作法．）
（2）若CD=6，AD=10，求AB的长．

分析 （1）根据角平分线的作图步骤画出图形即可；
（2）过点D作DE⊥AB于点E，先求出DE=DC=6，BC=BE，再根据AD=10，求出AE，设BC=x，则AB=x+8，根据勾股定理求出x的值即可．

解答 解：（1）作图如下：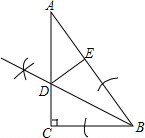


（2）过点D作DE⊥AB于点E，
∵DC⊥BC，BD平分∠ABC，
∴DE=DC=6，BC=BE，
∵AD=10，
∴AE=8，
∵BE=BC，
设BC=x，则AB=x+8，
∴在Rt△ABC中，由勾股定理得：
x2+162=（x+8）2，
解得：x=12，
∴AB=12+8=20．

点评 此题考查了勾股定理和尺规作图，用到的知识点是勾股定理、角平分线的性质，关键是作出辅助线，构造直角三角形．

练习册系列答案
相关题目
4．先化简，再求值：$\frac{x+1}{x-1}$-$\frac{{x}^{2}-2x}{{x}^{2}-1}$÷$\frac{{x}^{2}-x-2}{{x}^{2}+2x+1}$，其中x=2015．
13．观察下列式子的因式分解做法：
①${x^2}-1=\underline{（x-1）（x+1）}$
②x3-1
=x3-x+x-1
=x（x2-1）+x-1
=x（x-1）（x+1）+（x-1）
=（x-1）[x（x+1）+1]
=（x-1）（x2+x+1）
③x4-1
=x4-x+x-1
=x（x3-1）+x-1
=x（x-1）（x2+x+1）+（x-1）
=（x-1）[x（x2+x+1）+1]
=（x-1）（x3+x2+x+1）
…
（1）模仿以上做法，尝试对x5-1进行因式分解；
（2）观察以上结果，猜想xn-1=（x-1）（xn-1+xn-2+…+x2+x+1）；（n为正整数，直接写结果，不用验证）
（3）根据以上结论，试求45+44+43+42+4+1的值．
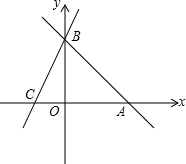10．直线AB：y=-x+b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．
（1）求点B的坐标；
（2）求直线BC的解析式；
（3）直线EF：y=2x+m（m≠0）交直线AB于E，交直线BC于点F，交x轴于点D，是否存在这样的直线EF，使得S△EBD=S△FBD？若存在，求出m的值；若不存在，请说明理由．
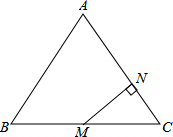17．如图，在△ABC中，AB=AC=5cm，BC=6cm，M为BC中点，MN⊥AC，垂足为N，
①连接AM，则AM与BC是什么位置关系？证明你的结论；
②求MN的长．
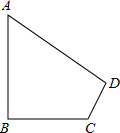7．如图，在四边形ABCD中，∠A=60°，∠B=∠D=90°，BC=6，CD=4，求AB的长．
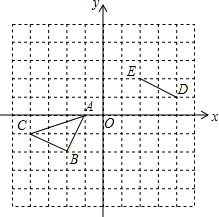14．如图所示的正方形网格中，△ABC的顶点均在格点上，线段DE的两个端点也在格点上，在所给直角坐标系中解答下列问题：
（1）试说明如何平移线段DE，使其与边BC重合？
（2）将△ABC绕坐标系中的某点P逆时针旋转180°，得到对应△FED，使边BC对应边为线段ED，请在图中画出△FED，并直接写出P点的坐标；
（3）在（2）中，线段AC在旋转过程中扫过的面积为8π．
11．恩施州城建部门计划对州城“工农路”实施改造，现有甲、乙两个施工队共同承担改造任务，已知甲队单独完成施工任务比乙队单独完成这项任务多用10天，且甲队施工45天与乙队单独施工30天的工作量相同：
（1）求甲、乙两个工程单独施工30天的工程各需多少天？
（2）若甲乙两队共同工作3天后乙队因另有任务而停止施工，剩下的部分由甲队继续直至完工，为了不影响工程进度，甲队的工作效率提高原来的2倍，若要求甲队的工作量不少于乙队的2倍，那么甲队至少还要单独施工几天？
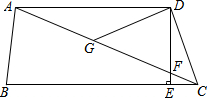12．如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD=2∠ACB．若DG=3，EC=1，则DE的长为2$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网