题目内容
5.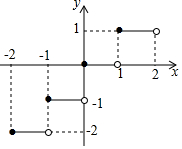 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )| A. | 0或$\sqrt{2}$ | B. | 0或2 | C. | 1或$-\sqrt{2}$ | D. | $\sqrt{2}$或-$\sqrt{2}$ |
分析 根据新定义和函数图象讨论:当1≤x<2时,则$\frac{1}{2}$x2=1;当-1≤x≤0时,则$\frac{1}{2}$x2=0,当-2≤x<-1时,则$\frac{1}{2}$x2=-2,然后分别解关于x的一元二次方程即可.
解答 解:当1≤x<2时,$\frac{1}{2}$x2=1,解得x1=$\sqrt{2}$,x2=-$\sqrt{2}$;
当x=0,$\frac{1}{2}$x2=0,x=0;
当-1≤x<0时,$\frac{1}{2}$x2=-1,方程没有实数解;
当-2≤x<-1时,$\frac{1}{2}$x2=-2,方程没有实数解;
所以方程[x]=$\frac{1}{2}$x2的解为0或$\sqrt{2}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了实数的大小比较.

练习册系列答案
相关题目
15.已知抛物线L:y=ax2+bx+c与抛物线L′:y=x2-2mx+4m+1关于直线x=2对称,且L′交y轴于点P(0,21),则方程ax2+bx+c=0的两个根为( )
| A. | x1=0,x2=3 | B. | x1=1,x2=-3 | C. | x1=3,x2=7 | D. | x1=-7,x2=-3 |
13.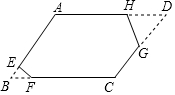 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
10.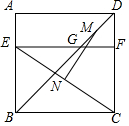 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
 如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 4 |


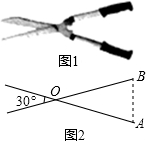 如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=75度.
如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=75度.