题目内容
7.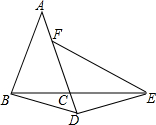 如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
分析 做出如图所示的辅助线,得到∠EDG=∠G,EG=BD,由AB=AC,BD=DE,得到∠ABC=∠ACB=∠ECG,∠DBE=DEB,由此推出∠G=∠ABD,由∠A+∠AFE=180°,∠EFG+∠AFE=180°,推出∠A=∠EFG,由此得到△ABD≌△FGE,即可推出结论.
解答 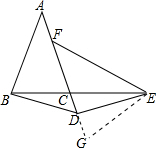 证明:在AD的延长线上取一点G,使EG=ED,
证明:在AD的延长线上取一点G,使EG=ED,
则∠EDG=∠G,EG=BD,
∵AB=AC,BD=DE,
∴∠ABC=∠ACB=∠ECG,∠DBE=∠DEB,
∴∠G=∠EDG=∠DEB+∠ECG=∠ABC+DBE=∠ABD,
∵∠A+∠AFE=180°,∠EFG+∠AFE=180°,
∴∠A=∠EFG,
在△ABD和△FGE中,
$\left\{\begin{array}{l}{∠A=∠EFG}\\{BD=EG}\\{∠ABD=∠G}\end{array}\right.$,
△ABD≌△FGE,
∴AD=EF.
点评 本题主要考查了等腰三角形的性质,全等三角形的判定与性质,正确做出辅助线是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=1,将△ABC绕点A顺时针旋转90°后得到△ADE,则BC边扫过部分图形(即阴影部分)的面积为$\frac{1}{4}$π(结果保留π).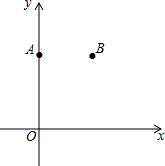 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8). 如图,A(-1,0),B(5,0),C(0,5),抛物线y=ax2+bx+c过A、B、C三点.
如图,A(-1,0),B(5,0),C(0,5),抛物线y=ax2+bx+c过A、B、C三点.