题目内容
2.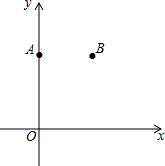 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
①点P到A、B两点的距离相等;
②点P到∠xOy的两边距离相等.
(2)在(1)作出点P后,直接写出直线PA的解析式.
分析 (1)点P到A、B两点的距离相等,说明点P在线段AB的垂直平分线上,点P到∠xOy的两边距离相等,说明点P在∠xOy的平分线上,两条线的交点即为点P;
(2)由线段AB的垂直平分线,得点P的横坐标为3,点P在第一象限的角平分线上,得点P(3,3),连立AP,可以求出直线解析式.
解答 解:(1)作图如下,点P即为所求作的点;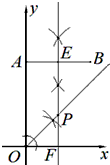
(2)y=-$\frac{5}{3}$x+8
∵点P到A、B两点的距离相等,
∴点P在线段AB的垂直平分线上.
∴点P横坐标为3,
∵点P到∠xOy的两边距离相等,
∴点P在∠xOy的平分线上,即在直线y=x上,
∴点P的坐标(3,3)
设直线PA解析式为y=kx+b(k≠0,k、b为常数),
将点P(3,3)、A(0,8)代入得:
$\left\{\begin{array}{l}{3=3k+b}\\{b=8}\end{array}\right.$
k=-$\frac{5}{3}$,b=8
∴直线PA的解析式为:y=-$\frac{5}{3}$x+8.
点评 题目重点考查尺规作图,包括垂直平分线、角平分线的尺规作图,学生掌握课本的基本尺规作图就可以画出点P,题目同时考察一次函数解析式,学生掌握待定系数法就可以.题目整体较为简单.

练习册系列答案
相关题目
11. 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
 如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )
如图,河堤横断面迎水坡AB的坡比是1:$\sqrt{3}$,堤高BC=10m,那么此拦水坝斜坡AB的坡度及坡面AB的长分别为( )| A. | $\frac{\sqrt{3}}{3}$,20m | B. | $\sqrt{3}$,10$\sqrt{3}$m | C. | 30°,20m | D. | 60°,10$\sqrt{3}$m |
12.某同学骑车从学校到家,每分钟行150米,某天回家时,速度提高到每分钟200米,结果提前5分钟到家,设原来从学校到家骑x分钟,则列方程为( )
| A. | 150x=200(x+5) | B. | 150x=200(x-5) | C. | 150(x+5)=200x | D. | 150(x-5)=200x |
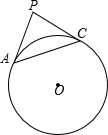 如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.
如图,已知⊙O的半径是4,AC是⊙0的弦,AP是⊙0的切线,AC=4$\sqrt{2}$,AP=4,连接PC,判断直线PC和⊙0的位置关系,并说明理由.
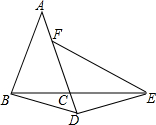 如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC的延长线上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD. 如图中以点A为端点的线段有4条,分别是AB、AE、AD、AC.
如图中以点A为端点的线段有4条,分别是AB、AE、AD、AC.