题目内容
2.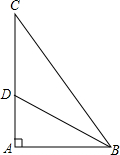 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8.
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8.
分析 在直角△ABD中利用勾股定理求得AD的长度.首先过点D作DE⊥BC于E,根据角平分线的性质,即可得DE=AD,即可求出答案.
解答  解:如图,在直角△ABD中,∠A=90°,AB=15,BD=17,则由勾股定理得到:AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{1{7}^{2}-1{5}^{2}}$=8.
解:如图,在直角△ABD中,∠A=90°,AB=15,BD=17,则由勾股定理得到:AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{1{7}^{2}-1{5}^{2}}$=8.
过点D作DE⊥BC于E,
∵在Rt△ABC中,∠A=90°,BD平分∠ABC,
即AD⊥BA,
∴DE=AD=8,
∴点D到BC的距离是8.
故答案是:8.
点评 此题考查了角平分线的性质的应用.此题难度不大,注意数形结合思想的应用,注意掌握辅助线的作法.

练习册系列答案
相关题目
10.若一个角的余角是50°,则它的补角是( )
| A. | 140° | B. | 40° | C. | 130° | D. | 160° |
17. 如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
 如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )
如图,AB、CD相交于点O,AD∥CB,若AO=2,BO=3,CD=6,则CO等于( )| A. | 2.4 | B. | 3 | C. | 3.6 | D. | 4 |
14.能使两个直角三角形全等的条件是( )
| A. | 斜边相等 | B. | 两直角边对应相等 | ||
| C. | 两锐角对应相等 | D. | 一锐角对应相等 |
12.-2014的相反数是( )
| A. | -$\frac{1}{2014}$ | B. | $\frac{1}{2014}$ | C. | 2014 | D. | -2014 |
 如图,在?ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E.求证:四边形GFHE是平行四边形.
如图,在?ABCD中,过对角线的交点O作两条直线分别与AB,BC,CD,DA交于点G,F,H,E.求证:四边形GFHE是平行四边形.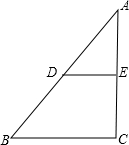 如图,Rt△ABC中,D、E分别是边AB,AC的中点,DE=3,AB=10,则AC=8.
如图,Rt△ABC中,D、E分别是边AB,AC的中点,DE=3,AB=10,则AC=8.