题目内容
1.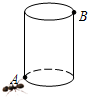 如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).
如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).
分析 根据题意得出蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,求出AC,BC,根据勾股定理求出AB即可.
解答  解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,
解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,
由题意得:AC=$\frac{5}{6}$π厘米,BC=12厘米,
由勾股定理得:AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{(\frac{5π}{6})}^{2}+{12}^{2}}$=$\sqrt{{(\frac{15}{6})}^{2}+{12}^{2}}$=$\frac{3\sqrt{89}}{2}$
(厘米).
答:沿圆柱侧面爬行的最短路程是$\frac{3\sqrt{89}}{2}$厘米.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆柱的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
10.正n边形的一个内角与正2n边形的一个内角和等于270°,则n等于( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |

 (1)下面是马虎同学解的一道题
(1)下面是马虎同学解的一道题
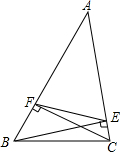 如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE.
如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE.