题目内容
19.已知∠ABC的边BA、BC分别与∠DEF的边ED、EF垂直,垂足分别是P、Q,且∠ABC=60°,求∠DEF的度数.分析 利用已知角的各边之间的关系进而分别画出符合题意的图形:图1根据等角的余角相等求解;图2根据四边形内角和等于360°求解.
解答 解:如图所示:
∵∠ABC=60°,
∴图1,∠DEF=60°,
图2,∠DEF=360°-90°-90°-60°=120°.
故∠DEF的度数是60°或120°.
点评 此题主要考查了多边形内角与外角,垂线的定义,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
10.正n边形的一个内角与正2n边形的一个内角和等于270°,则n等于( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
7.四边形ABCD中,如果AD∥BC,那么∠A:∠B:∠C:∠D可以等于( )
| A. | 5:1:2:4 | B. | 5:4:2:1 | C. | 5:2:4:1 | D. | 1:2:4:5 |
8.下列图形中不可能是正多边形的是( )
| A. | 三角形 | B. | 正方形 | C. | 四边形 | D. | 梯形 |

 动手操作,你需要哪些工具,能在数轴上找到π,试着画出.
动手操作,你需要哪些工具,能在数轴上找到π,试着画出.
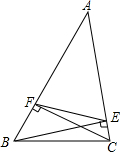 如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE.
如图,在△ABC中,BE、CF分别是AC、AB边上的高,∠A=45°,求S△AEF:S四边形FBCE.