题目内容
12．
矩形ABCD的对角线AC、BD相交于点O，∠AOD=120°，AC=8，则△ABO的周长为（ ）| A． | 12 | B． | 14 | C． | 16 | D． | 18 |
分析 由矩形的性质得出OA=OB，再证明△AOB是等边三角形，得出AB=OA=OB=4，即可求出△ABO的周长．
解答 解：∵四边形ABCD是矩形，
∴OA=$\frac{1}{2}$AC=4，OB=$\frac{1}{2}$BD，AC=BD，
∴OA=OB，
∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=OB=4，
∴△ABO的周长=OA+OB+AB=12；
故选：A．
点评 本题考查了矩形的性质、等边三角形的判定与性质；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．
练习册系列答案
同步轻松练习系列答案
相关题目
2．下列句子，不是命题的是（ ）
| A． | 两条直线平行，同位角相等 | B． | 直线AB垂直于CD吗？ | ||
| C． | 若|a|=|b|，那么a2=b2 | D． | 对顶角相等 |
7．
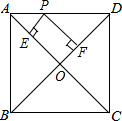如图，在正方形ABCD中，AB=4，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为（ ）
如图，在正方形ABCD中，AB=4，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为（ ）| A． | 2$\sqrt{2}$ | B． | 4 | C． | 4$\sqrt{2}$ | D． | 2 |
在平面直角坐标系xOy中，一次函数的图象经过点A（1，-3）和B（2，0）．